

摘要:在MEMS加速度计加速寿命试验及加速性能退化试验研究的基础上,对MEMS加速度计在振动环境下的可靠性技术进行了研究。通过理论分析MEMS加速度计在振动环境下的失效模式和失效机理,结合具体的试验条件设计了加速度计加速寿命试验及加速性能退化试验方案,并对MEMS加速度计在振动环境下的失效数据分别进行了加速寿命可靠性评估及加速性能退化可靠性评估。研究表明,两种评估方法得到的评估结果基本一致;加速性能退化评估方法适用于MEMS加速度计在振动环境中的可靠性研究,且该方法简捷、正确可行、节省试验费用,为MEMS加速度计在实际应用中提供了重要的参考依据。
微电子机械系统(MEMS)在近十几年来取得了飞速的发展,微加速度计是MEMS的一个重要分支,在航空、航天、汽车、国防等领域有着广泛的应用。随着高新技术的发展,现代武器装备的使用环境越来越严酷,对质量和可靠性的要求也越来越高,MEMS加速度计的可靠性保障越来越困难。MEMS加速度计的可靠性问题已成为阻碍它在武器系统中广泛应用的重要因素之一,因此,MEMS加速度计的可靠性研究对于提高MEMS器件的性能、实现其市场化具有极其重要的意义。
国内MEMS加速度计研究的主要单位有清华大学、北京大学、东南大学、电子13所、电子49所、航天771和中北大学等。在研制过程中,国产加速度计暴露出了不同的可靠性问题:如振动冲击环境下微结构断裂问题、零偏问题、温度漂移问题、偏置稳定性问题等等,有的微加速度计甚至在基本测试合格放置一段时间后仍发生问题。要满足大批量国产MEMS加速度计应用于国防领域多方面的实际需求,开展振动环境下MEMS加速度计的可靠性研究并将研究结果应用于MEMS加速度计的设计和制作过程已势在必行。
1 MEMS加速度计的结构及原理
本文研究的MEMS加速度计为压阻式硅微加速度计,量程为10 gn,其结构如图1所示。MEMS加速度计是由悬臂梁和质量块以及布置在梁上的压阻组成,呈双端四梁结构。
图1 加速度计结构示意图
MEMS加速度计可简化为由弹簧、阻尼器、质量块构成的二阶单自由度振动系统,如图2所示。
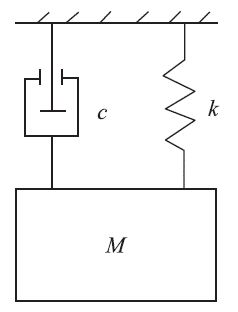
图2 压阻式微加速度计模型
当有加速度输入时,质量块由于惯性力作用而发生位移,位移变化量与输入加速度的对应关系,可以描述为一个单自由度二阶弹簧阻尼振动系统,系统的数学模型即为:
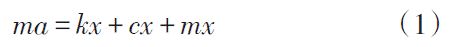
式中,k为等效弹性系数,c为等效阻尼系数,m为等效惯性质量,a为输入加速度。可以求出位移量和输入加速度的关系公式:
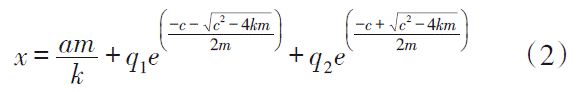
其中,q1和q2是积分常数,决定系统的边界条件。
2 MEMS加速度计在振动环境下的失效分析
振动对MEMS加速度计的主要影响是对MEMS加速度计的结构造成损坏。主要是产生裂纹、断裂(如图3所示)、磨损、分层和由于振动产生的交变应力超过MEMS加速度计所能承受的弹性极限应力而造成的破坏,以及长时间振动的交变应力造成的累积损伤,使MEMS加速度计发生疲劳损坏等。
疲劳是材料在交变载荷作用下损伤逐渐累积并最终导致结构失效的力学行为。循环加载一个低于MEMS加速度计材料屈服强度或断裂强度的振动载荷,这种载荷将在MEMS加速度计的表面产生一个微裂纹,随着时间变化,将在这一区域发生塑性变形,最终导致结构发生损坏,由于MEMS加速度计设计缺陷,梁的根部应力最大,所以断裂一般首先发生在梁的根部。疲劳破坏是一个渐进的、累积的过程,疲劳损伤将消耗微加速度计的寿命。疲劳特性可以用S-N疲劳曲线来描述,如图4所示。
图3 振动导致MEMS加速度计的结构发生破坏
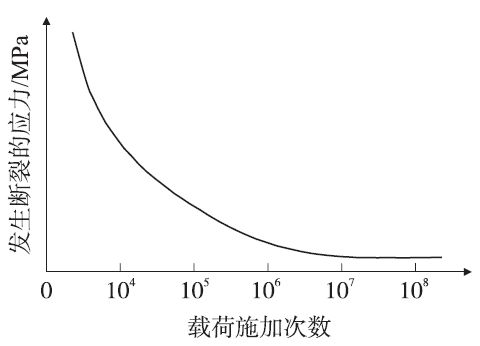
图4 材料的S-N曲线
3 MEMS加速度计在振动应力下的试验
采用振动环境下的加速寿命试验,来加速暴露试验样品的缺陷和薄弱点,从而使暴露故障的时间大大短于正常可靠性应力条件下的所需时间。根据MEMS加速度计的工作极限,确定3个振动恒定应力量值分别为30 gn、35 gn、40 gn,按图5所示的恒定应力试验剖面进行恒定应力试验。试验样品:9个结构相同,量程为10 gn的同批次加工的压阻式MEMS 加速度计;振动载荷:由TV5200多功能校准试验装置提供如图6所示,9个样品的失效时间见表1。当检测到MEMS 加速度计零位输出超出2.4 V ~ 2.6 V范围时认为加速度计失效。无输出,输出曲线有明显偏差,电路板出现裂纹,元器件出现松动等现象均认为加速度计失效。在加速退化试验测试过程中,试验数据呈现退化现象,截取试验开始到试验tn时间MEMS加速度计的输出电压检测值(未出现异常)如表2所示,输出电压与时间的关系如图7所示。
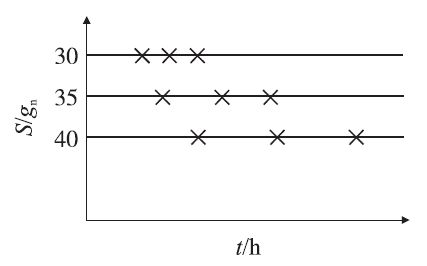
图5 振动恒定应力试验剖面图

图6 振动试验装置图
表1 加速度计在各振动应力下的失效时间

表2 MEMS加速度计输出电压检测值
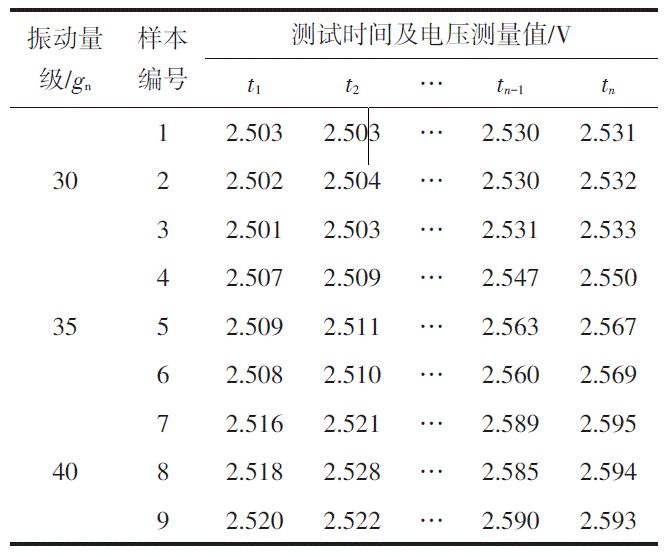
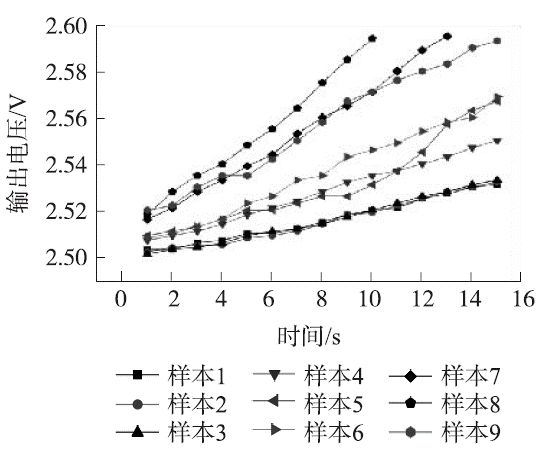
图7 输出电压的测试数据
4加速度计的寿命评估
4.1建立基于加速寿命数据的加速模型
对表1的失效寿命数据进行分布假设检验,选择拟合最好的(AD 值较小)的Weibull 分布,分布的概率图如图8所示,由图可知,每个应力对应的失效次数基本分布在一条直线上,且不同应力下的直线近似平行,呈现出平移加速情形,说明MEMS加速度计在加速寿命试验的过程中失效机理未发生变化。
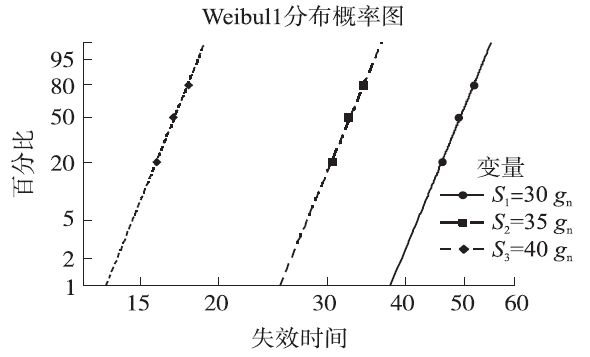
图8 失效寿命的分布检验结果
根据表1列出的3个恒定冲击应力下样本的失效冲击次数,运用最小二乘法统计计算得到Weibull分布下的参数估计值,结果如表3所示。
表3 Weibull分布的参数估计值

对于振动作为加速应力的加速寿命试验,其加速模型可用逆幂率模型来描述,产品平均寿命η与振动应力S的关系为:

两边取对数有:

采用逆幂律模型建立尺度参数η的加速模型,如图9所示,其表达式如下:
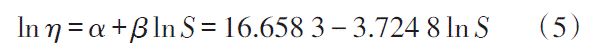
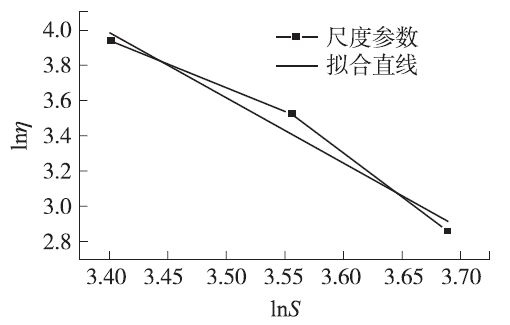
图9 尺度参数的加速方程
4.2建立基于性能退化试验数据的加速模型
根据加速度计的实际应用要求,将失效判据设为输出电压值超过2.6V。对表2所示的退化数据进行拟合,当样本的输出电压值等于失效阈值Df=2.6 V时,记录失效寿命时间如表4所示。得到伪失效寿命数据后,建立加速模型的方法同上,得到加速方程如式6所示:
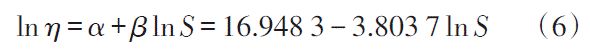
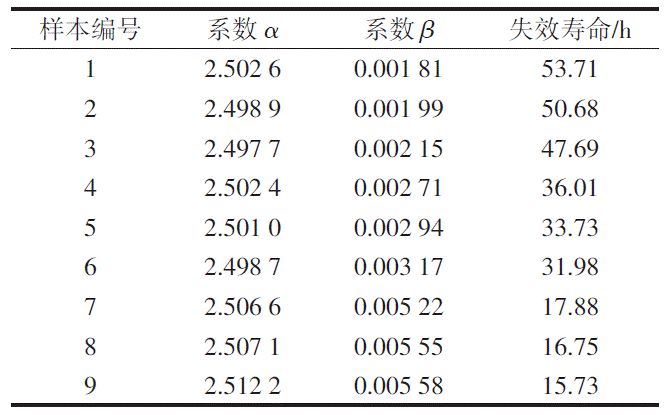
表4 各样本性能退化模型参数估计与失效寿命
4.3寿命评估
由于陆地运输环境主要由车体的支撑和结构同路面平度作用而引起的宽带随机振动组成。一般来说,拖车的振动谱具有突出的随机性,在各种离散频率外还有很多峰和谷。这种环境可以用类似于GJB150.16-86 中图34的谱进行模拟,取S0=7.698 gn。根据式5求得的加速模型,基于加速寿命试验结果外推正常使用条件下的参数为:
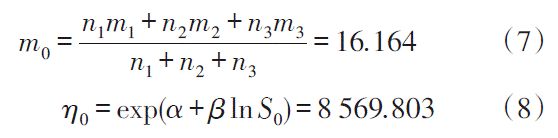
可靠度函数为:
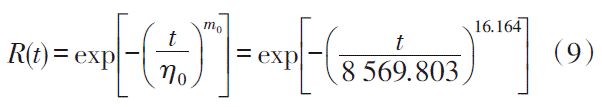
根据式(6)求得的加速模型,基于加速性能退化试验结果外推正常使用条件下的参数为:
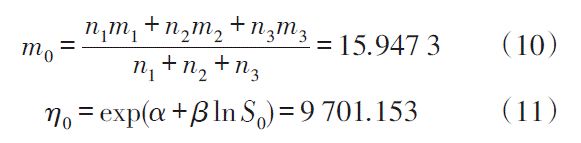
可靠度函数为:
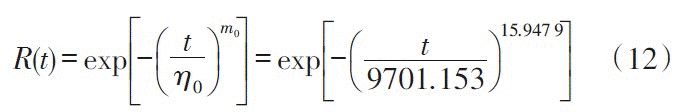
图10所示,为使用两种可靠性评估方法外推得到的可靠度曲线,分别为MEMS 加速度计样本基于加速寿命和基于退化轨迹时的可靠度曲线。由图可知,两种假设分布得到的可靠度曲线形状比较接近,验证了采用两种方法对MEMS 加速度进行可靠性评估的可行性;由于加速寿命评估通过获取高应力下的失效寿命时间来折算正常应力下的失效时间,故其评估结果较性能退化评估结果更精确。
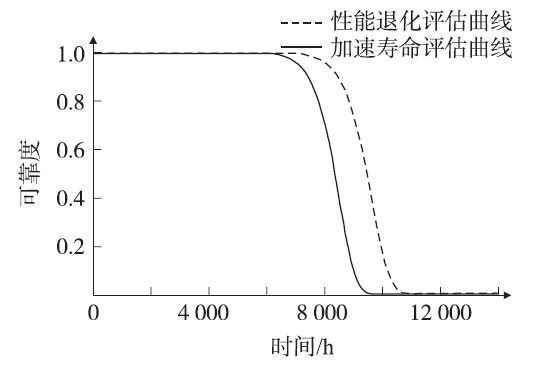
图10 可靠度曲线
5结论
本文根据MEMS加速度计的应用背景,提出了振动应力下MEMS加速度计的加速寿命评估方法和加速性能退化评估方法。综合比较:加速寿命评估方法适用于容易获取失效寿命的情况,计算过程简单,计算结果更精确;加速性能退化评估方法能够充分应用测试过程提供的寿命信息,节省了试验时间及试验费用,但该方法需要根据退化轨迹模型外推伪失效寿命,可能会影响评估精度。试验和评估结果表明:两种方法能有效的评估MEMS加速度计的寿命,且其简捷易行,可信度高,为MEMS加速度计在实际应用中提供了重要的参考依据。
全部0条评论

快来发表一下你的评论吧 !
