

有符号数的计算在 Verilog 中是一个很重要的问题(也很容易会被忽视),在使用 Verilog 语言编写 FIR 滤波器时,需要涉及到有符号数的加法和乘法,在之前的程序中我把所有的输入输出和中间信号都定义成有符号数,这样在计算时没有出现问题(实际在之前的程序中遇到了问题,最后滤波结果不对,博客的程序是已经改正过的),下面实际试验一下 Verilog 的乘法问题;
1. 编写程序测试无符号数和有符号数的乘法
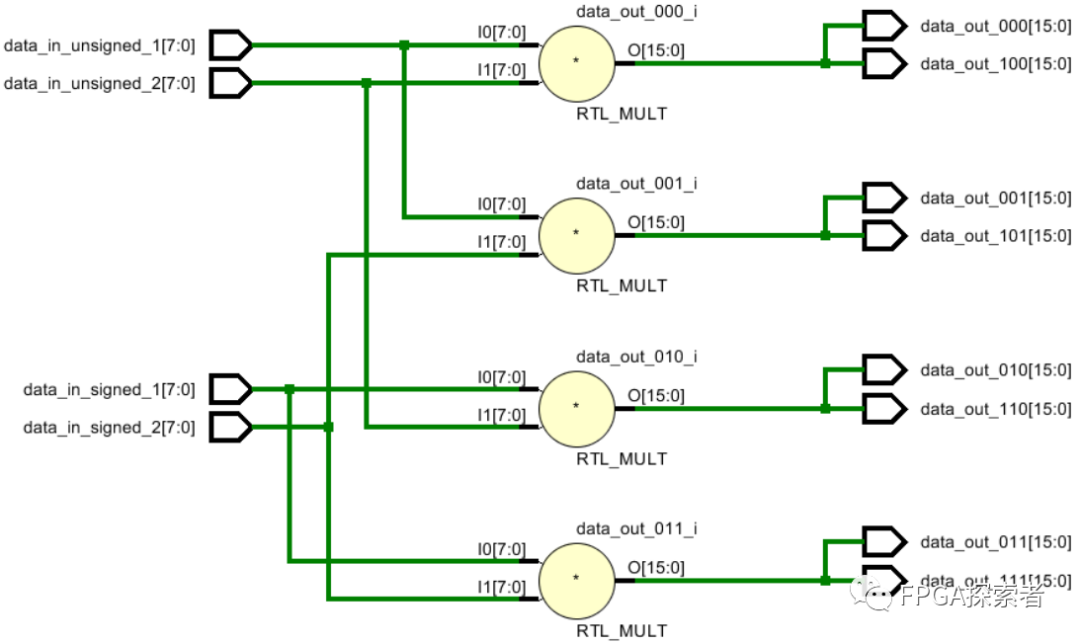
编写程序如下,其中,乘法的两个乘数分别是无符号、有符号的四种组合,输出的积也是分为无符号和有符号,共计 8 种可能;
module signed_test( input [7:0] data_in_unsigned_1, input [7:0] data_in_unsigned_2,
input signed [7:0] data_in_signed_1, input signed [7:0] data_in_signed_2,
output [15:0] data_out_000, output [15:0] data_out_001, output [15:0] data_out_010, output [15:0] data_out_011,
output signed [15:0] data_out_100, output signed [15:0] data_out_101, output signed [15:0] data_out_110, output signed [15:0] data_out_111 );
//无符号 = 无符号 * 无符号assign data_out_000 = data_in_unsigned_1 * data_in_unsigned_2;//无符号 = 无符号 * 有符号assign data_out_001 = data_in_unsigned_1 * data_in_signed_2;//无符号 = 有符号 * 无符号assign data_out_010 = data_in_signed_1 * data_in_unsigned_2;//无符号 = 有符号 * 有符号assign data_out_011 = data_in_signed_1 * data_in_signed_2;
//有符号 = 无符号 * 无符号assign data_out_100 = data_in_unsigned_1 * data_in_unsigned_2;//有符号 = 无符号 * 有符号assign data_out_101 = data_in_unsigned_1 * data_in_signed_2;//有符号 = 有符号 * 无符号assign data_out_110 = data_in_signed_1 * data_in_unsigned_2;//有符号 = 有符号 * 有符号assign data_out_111 = data_in_signed_1 * data_in_signed_2;
endmodule
生成的 RTL 图如下:
可以看到,输出的积和符号无关,有符号数和无符号数实际上是同一个数,只看我们怎么定义它,比如乘积是 16 位的二进制 16’b1100_0000_0000_0011,当我们认为它是无符号数是,最高位的 1 就不是符号位,而是 2^15(2的15次方),这样这个数代表的十进制是 2^15 + 2^14 + 2^1 + 2^0 = 49155;
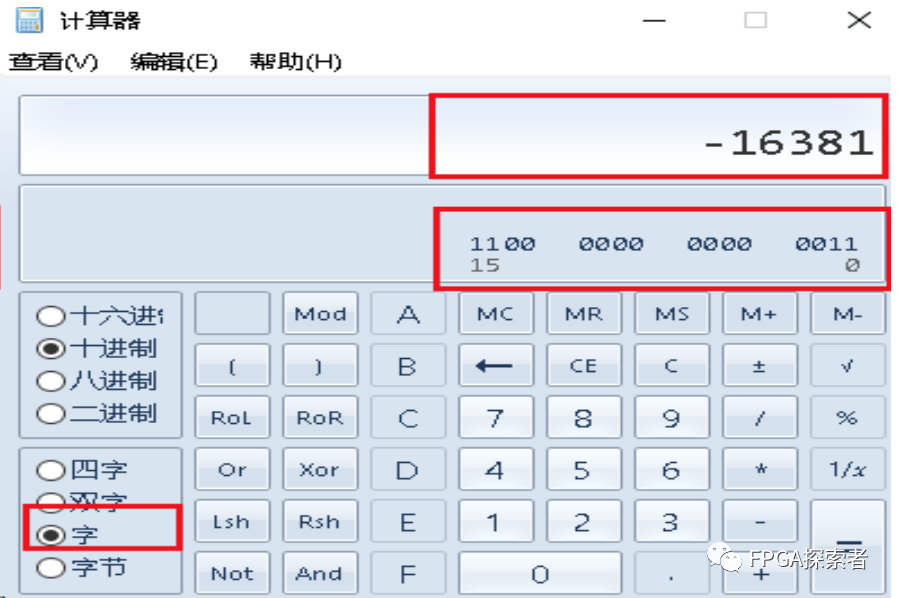
如果把 16 位的二进制 16’b1100_0000_0000_0011 当成是一个有符号数来看,那么最高位是符号位,且剩下的数据时原来的数据二进制表示后取反再加1(补码表示),要计算它对应的十进制数
(1) 先去掉符号位,保留剩下的 15-bit 的 100_0000_0000_0011;
(2) 把 100_0000_0000_0011 取反,得到 011_1111_1111_1100;
(3) 把 011_1111_1111_1100 的最低位 + 1,得到 011_1111_1111_1101;
(4) 011_1111_1111_1101 按照无符号数换算成十进制是 16381;
(5) 把最高位符号位加上,0代表正数,1代表负数,所以最后换算是 -16831;
Windows 计算器默认最高位是符号位;
测试数据如下:
initial begin data_in_unsigned_1 = 8‘hff; //255 data_in_unsigned_2 = 8’hf0; //240 data_in_signed_1 = 8‘hff; //-1 data_in_signed_2 = 8’hf0; //-16 #200; data_in_unsigned_1 = 8‘hff; //255 data_in_unsigned_2 = 8’h0f; //15 data_in_signed_1 = 8‘hff; //-1 data_in_signed_2 = 8’h0f; //15 #200; data_in_unsigned_1 = 8‘d127; //127 data_in_unsigned_2 = 8’d15; //15 data_in_signed_1 = -8‘sd127; //-127,十进制有符号数赋值,必须要用 sd 表示 data_in_signed_2 = -8’sd15; //-15 #200; data_in_unsigned_1 = 8‘d128; //128 data_in_unsigned_2 = 8’d15; //15 data_in_signed_1 = -8‘sd128; //-128 data_in_signed_2 = -8’sd15; //-15 #200; data_in_unsigned_1 = 8‘d127; //127 data_in_unsigned_2 = 8’d15; //15 data_in_signed_1 = -8‘sd127; //-127 data_in_signed_2 = 8’sd15; //15 #200; data_in_unsigned_1 = 8‘d128; //128 data_in_unsigned_2 = 8’d15; //15 data_in_signed_1 = -8‘sd128; //-128 data_in_signed_2 = 8’sd15; //15 #200; data_in_unsigned_1 = 8‘d127; //127 data_in_unsigned_2 = 8’d15; //15 data_in_signed_1 = 8‘sd127; //127 data_in_signed_2 = -8’sd15; //-15 #200; data_in_unsigned_1 = 8‘d127; //127 data_in_unsigned_2 = 8’d15; //15 data_in_signed_1 = 8‘sd127; //127 data_in_signed_2 = 8’sd15; //15 #200; $stop;end
2. 仿真分析
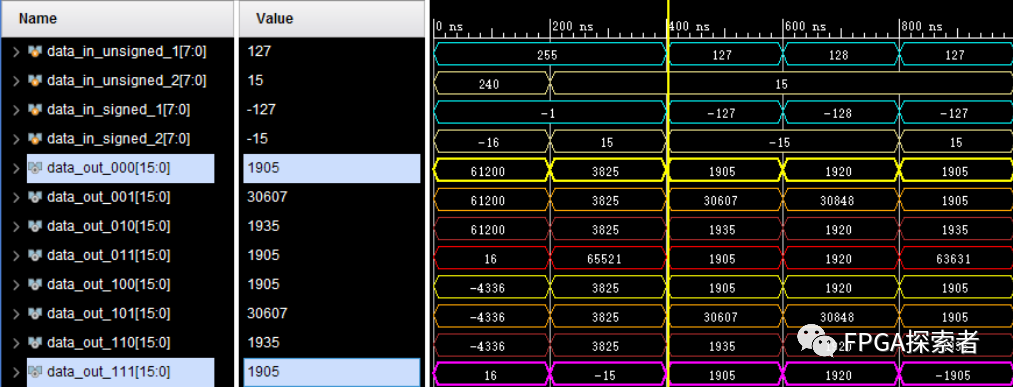
计算的结果仿真如下:
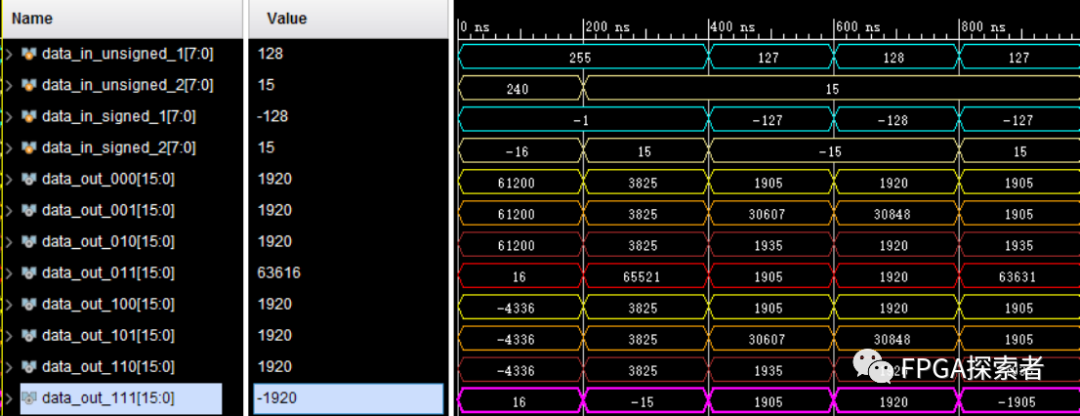
对上图分析:
(1) 在 0 ~ 400 ns,仿真中使用十六进制赋值相同的十六进制数据给乘数,让乘数分别以无符号数和有符号数进行读取,可以看到对 8’hff(对应二进制 8’b1111_1111)以无符号数读取时是按照 原码 读取,对应十进制 255,以有符号数读取时是按照补码读取,按照上文所说的去掉符号位后取反、加1再计算十进制得 -1;
(2) 直接赋值十进制数据,乘数在以无符号数读取时时按照原码读取,127就对应 8 位二进制数 8’b0111_1111,十进制 128 就对应 8 位二进制 8’b1000_0000;而以有符号数读取的时候是会直接转换为补码形式,如 -127,先去掉符号位是 127,对应 7 位二进制数 7’b111_1111,取反为 7’b000_0000,加 1 为 7’b000_0001,将符号位补回到最高位为 8’b1000_0001;对于 -128 的表示比较特殊,8-bit的二进制数最高位是符号位,表示正负,剩下的 7-bit 能够表示的数的范围是 0 ~ 127,前面加上 ± 就能表示 -127 ~ 127,其中有 2 个数很特殊就是 8’b0000_0000 和 8’b1000_0000,按照上面会出现 +0 和 -0,为了区分出这两个数,前人定义 8’b0000_0000 表示 0,而 8’b1000_0000 表示 -128,这样不仅能区分开两个数,还多表示了一个数 -128(整个计算机体系通用,其他位数时类似表示一个负数);
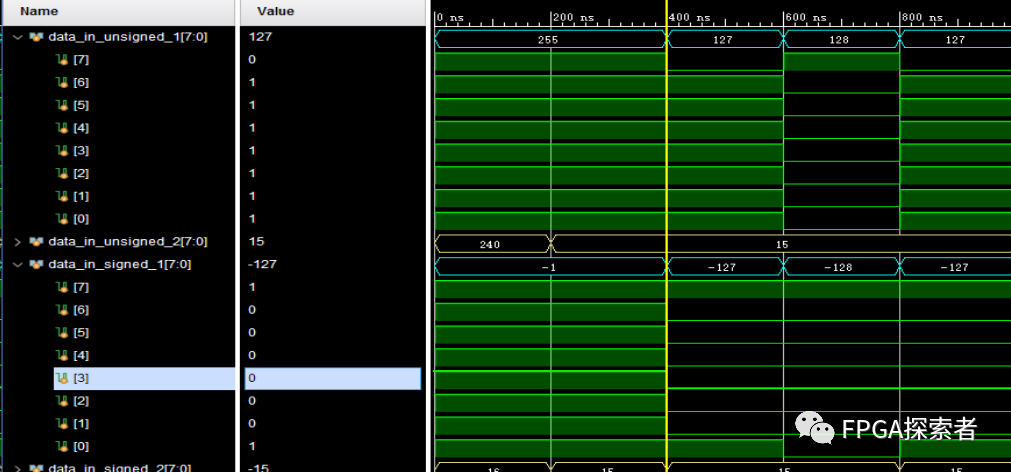
(3) 实际上,观察下图数据可以发现,只有data_out_000 和 data_out_111 的数据时全部计算正确的,这也符合常理:
无符号 * 无符号 = 无符号;
有符号 * 有符号 = 有符号;
其它的计算为什么会出错呢?实际上这里遵循一个原则:
如果表达式中有一个无符号数,则所有的操作数都会被强行转换为无符号数;
这样也就解释了 0 ~ 400 ns 时的 data_out_001 和 data_out_010 的计算结果和 data_out_000 完全一致,它们都是把赋值的 8 位十六进制数当做无符号数计算的(这里不存在十进制到二进制原码、补码换算的问题,因为给的是十六进制);
当后面设计输入输出时,如果是有符号,那么将相关计算的输入/输出和中间量都显式的用 signed 定义;
3. 有符号数乘法的另一种计算
前面说的计算时将涉及到的相关量全部定义为有符号数是一种计算方法,此外,通常情况下可能会定义的无符号数,但是实际传入的是有符号数,比如下面的输入和输出都没有指定成 signed 有符号数,计算时默认是按照无符号数计算(实际上我感觉是把读取到的 8 位二进制数当做原码去算),此时若外部传入的数据实际上是有符号数(比如 FIR 滤波器传入了正负均有的待滤波信号),那么需要对符号位进行扩展来计算乘法和加法;
module signed_test_2( input [7:0] data_in_1, input [7:0] data_in_2, output [15:0] data_out_1, output [15:0] data_out_2);
对于乘法,需要扩展符号位 到 和积的位数相等,比如乘数a为 N-bit,乘数 b 为M-bit,两个相乘得到 N+M 位数据,此时需要对 a 扩展 M-bit 到 N+M 位,对 b 扩展 N-bit 到 N+M 位;
下面,使用 位拼接符 { } 来做演示,位拼接符可以按照二进制的位来进行高低位的拼接,假设 data_in_1= 8’b1000_0011,对于 {{8{data_in_1[7]}},data_in_1} 可以这样理解:
(1) 先看 8{data_in_1[7]},表示取出 8-bit 数据 data_in_1 的最高位 data_in_1[7],重复 8 次,相当于 { data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7], data_in_1[7] },即高位扩展 8-bit 的 1
(2) {{8{data_in_1[7]}},data_in_1} 相当于在 data_in_1 的前面补上 8 个 data_in_1[7],即 结果为 16-bit 的 16’b1111_1111_1000_0011;
//不做符号位扩展,直接相乘assign data_out_1 = data_in_1 * data_in_2;//做符号位扩展,再相乘assign data_out_2 = {{8{data_in_1[7]}},data_in_1} * {{8{data_in_2[7]}},data_in_2};
仿真测试数据如下,1 处用十六进制给出数据,2 处用有符号的十进制赋值,3 处是为了和 2 处对比,看最后赋值是否一样(看到有博客说 3 的赋值是错的,所以测试一下);

仿真结果如下,可以看到上图 2 处和 3 处的赋值在仿真时是同样的数据,把所有数据都用有符号的十进制数显示(右键数据 Radix -》 Signed Decimal);
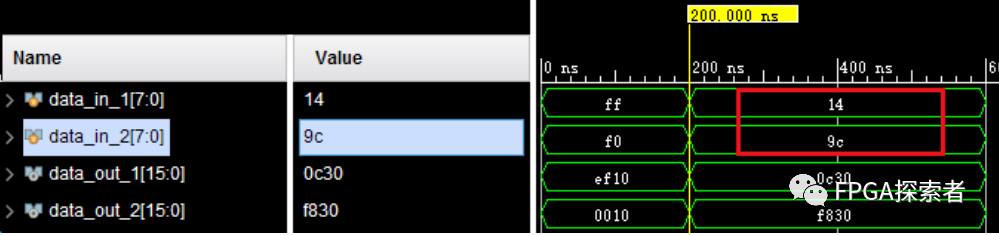
可以看到,data_out_1的结果是错的(没有补符号位),data_out_2的结果是对的(补符号位);
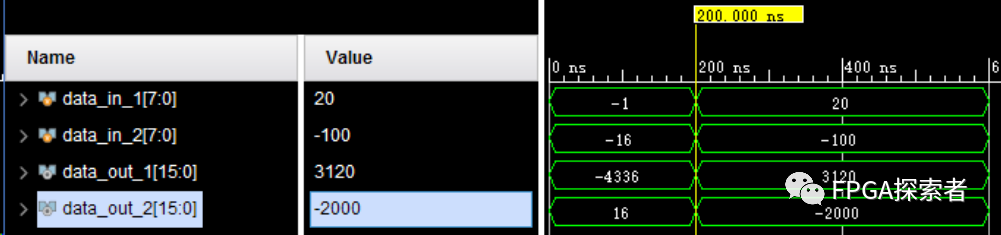
对有符号数的加法,同样的,要么相关的运算全部定义成有符号数,要么进行符号位的扩展,对于加法操作,只需要每个被加数扩展 1 位符号位即可;
除此之外,还可以调用乘法器的 IP 来代替 乘法符号 *,或者加法器的 IP 来代替 加法符号 +,在 IP 核中配置输入输出为有符号数即可。
编辑:lyn
全部0条评论

快来发表一下你的评论吧 !
