

电子说
由于直接变频信号链上使用了IQ解调器,因此要精确地预测噪声指数的影响通常较为困难。一般使用噪声指数仪来测量噪声指数,然而,这种仪器不能在极低的频率下工作,因而无法在基带频率范围内捕获典型的噪声数据。一种可行的方法是使用校准噪声源和带前置放大输入的频谱分析仪对解调器中的噪声进行测量,该方法受限于频谱分析仪在基带频率上的灵敏度,在实际应用中,可以配合使用矢量信号分析技术来评估基带噪声。
本文将介绍在有干扰信号和无干扰信号的两种情况下,使用基带矢量信号分析仪测量IQ解调器噪声指数的一些基本技术。
背景
假定直接变频信号链如图1所示,如众多接收机一样,该设计在正交混频处理、信道选择和信号检测之前使用了一个频段可选的低噪声前端。这类似于一个真实的中频采样接收机,除了信号通过IQ解调器时,被分解成正交的两部分,这具有为初始IQ矢量(用于产生有用调制信号)提供直接输出的固有便利性,认识到该固有特性的存在有利于理解该正交混频处理及与其相关的复数运算。
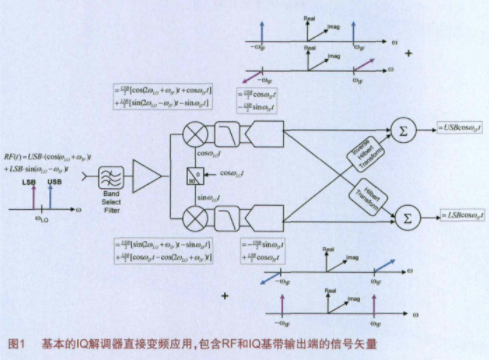
假设RF输入信号由以下表达式给定:
RF(t)=USB•(cos(ω_{LO}+ω_{IF})t+LSB•sin(ω_{LO}-ω_{IF})t
这时,USB为随时间变化的上边带包络,而LSB为下边带包络。
当信号通过解调器内核时,它将与本振(LO)信号进行混频。将本振信号通过90°的移相器,既可以获得与其同相的分量(余弦),也可以得到与其正交的分量(正弦)。而将本振信号乘以RF信号,则会产生高频项和低频项,这时使用低通滤波器就可把信号的高频项过滤掉。该信号的定量关系与复频谱如图1所示。
如图所示,同相和正交分量均包含USB和LSB分量。如果同相信号经过希尔伯特变换,所有的负频率就会获得+90°相移,而正频率获得-90°相移。因此,当它们与正交分量相加时,USB信号就会被抵消掉,而只剩下LSB信号。同样地,我们可以对正交信号进行希尔伯特反变换,并将其与同相信号分量相加。这样,我们就可以获得USB信号,而抑制LSB信号,这就是镜频抑制的本质,显然,正交的精确度决定了抑制度的高低。应该注意的是,在正交求和网络之前,有用信号和镜像信号会发生重叠而造成上、下边带难以区分。
如果我们假设一个零中频条件(ωIF=0),就会发现可以很容易地在希尔伯特正交求和网络的输出端获得USB和LSB矢量。
如果初始信号为IQ正交调制信号,其由如下表达式给出:
RF(t)=I(t)•cosω_{LO}t+Q(t)•sinω_{LO}t
我们将会发现I、Q矢量在正交求和网络的输出端出现。因此,使用被调谐到载波频率的本振,IQ解调器就可以直接解调出IQ调制信号。
噪声的考虑因素
噪声指数(以分贝表示)用来度量信号通过有噪声的设备后,信噪比(SNR)的降低程度,即SNRINPUT/SNROUTPUT,或等于10log(F),这里F为噪声系数。在频率转换过程中,了解信号源中信号和噪声的混频过程尤为重要。一般噪声指数的测量是通过在噪声指数仪上,观察位于设备线性信号增益之上的噪声基底的上升情况。
在混频处理中呈现的问题表现为两个部分,测量不同频率上的输出噪声是首要任务,比测量输入端的源噪声更有必要,这需要对噪声接收机和噪声源进行仔细的校准。其次,传送到中频输出频率的噪声是上边带和下边带噪声的共同结果,称为双边带噪声指数测量。当检测图1中的希尔伯特网络前的数字信号时,该噪声会非常明显,注意在解调器输出端上、下边带的情况。
由于各边带的变频增益不一定相同,这将会令测量复杂化,而这时尝试预测单边带的噪声指数也会显得有点困难。实际当中,使用镜频抑制方案可有效消除来自无用边带(镜频)的噪声或干扰。而在宽广的可变频率范围内的测量,可能无法对单一边带的噪声指数实施测量,除非混频处理能提供足够的镜像抑制性能。
矢量信号分析
矢量信号分析是用于评估已调信号的调制精度的一种技术。大多数矢量信号分析仪(VSA)有基本的频谱分析功能,具备解调信号并报告该已调信号的各种信息的能力。然而已调信号可以使用调幅、调相或两者结合的调制方式。VSA是专为分析用于描述波形的信号矢量的精确度而设计的,而其通常被用来测量误差矢量。
通过测量各个传输码元的幅度和相位,VSA可以计算出被测矢量及其最邻近的理想星象点之间的误差矢量。为了确定理想星象图的坐标,首先必须为VSA指定合理的波形特性(诸如码元速率、脉冲成形滤波器规格和调制方式等)。如果误差矢量幅度(EVM)过大而使得VSA无法正确地消除预期的码元矢量,结果将会是有噪的且非常不可靠,在诸如高阶QAM调制等密集调制方案中类似情况尤为严重。
在时域采样系统中,EVM可以定义为:
EVM=sqrt{frac{sum_{k=1}^{M}|Z(k)-R(k)|^{2}}{sum_{k=1}^{M}|R(k)|^{2}}}
这里,Z(k)是复合接收信号矢量,它包括了同相(I)和正交(Q)两个部分;而R(k)是理想复合参考矢量。误差矢量幅度是衡量接收机性能好坏的一个测度标准,其等于误差矢量的RMS功率与参考矢量的RMS功率的比值。
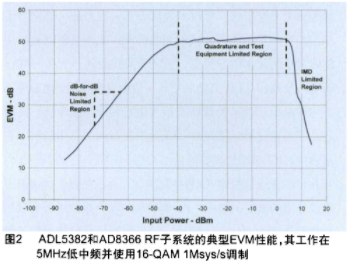
如图2所示,相对于接收到的输入信号功率,接收机会呈现三个显著的EVM界限。由于接收机的非线性度,当信号电平较高时失真部分会落入带内,且EVM性能衰退会随着信号电平的增加而显著加剧。在中等信号电平范围内,接收机表现比较线性,而且信号远高于其它显著噪声成分。
EVM这时趋向于获得最佳的水平,而这主要由解调器的正交精度和测试设备的精度来决定。当信号电平减弱而噪声成为主要成分时,随着信号电平的下降EVM性能也将会有所衰退。在低信号电平下,噪声成为主要限制,EVM分贝值将会与SNR比值成正比。利用这个关系,有可能估算出接收机的输入参考噪声电平和计算出噪声指数。
解调器噪声指数的测量
图3描述的是利用VSA来实现解调器特性测量的配置。负责为测试设备(DUT)馈送输入信号的合成网络允许同时使用多个测试信号。而为了确定解调器输入端的绝对功率电平,需要对一直到隔离器和合成器的整个信号路径进行校准。该配置能够在多种阻塞情况下进行性能测试。
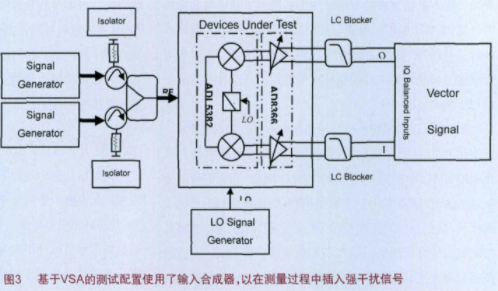
在强干扰条件下测量性能降低程度对分析工程师来说是一项非常大的挑战。强干扰情况即是指当邻近有强干扰源时,依然需要解调出微弱的有用信号。阻塞测试是各种蜂窝和点对点空中接口标准的通用要求。阻塞源可能来自于相同蜂窝半径范围内的其他无线终端,或者是邻近基站用作蜂窝小区识别的导频音。
直接变频接收机直到信号通过低噪声前端和IQ解调器后才具备信道选择特性。这迫使该前端和解调器能够处理所有信号电平的无用强干扰,同时还必须维持足够的灵敏度以成功恢复微弱的有用信号。在基带中,IQ信道选择滤波器经常用于衰减邻近的强干扰信号并传送有用信号到IQ数字化ADC。
为了在强干扰情况下确保适当的级联灵敏度,IQ解调器的噪声指数经常会吸引系统设计师的关注。该衰减必须是可测量且可控制的。频率转换器件在大信号激励情况下容易造成噪声指数性能的降低。因为在无用强干扰信号上,本振相位噪声会相互混频,因此这种情况只是局部性的。然而在时域里,混频器起到乘法器的作用,使本振的相位特性与强干扰信号发生卷积。
强干扰离有用信号越近,振荡器相位激起的一些能量越可能会在重要的信号频带内出现。另外一种机制还包括混频器内固有闪烁噪声的干扰调制。强干扰信号的RF牵力可导致在混频器内的晶体管结合处产生平方级的直流偏移。这个受制于直流偏移的信号电平可以重新偏置晶体管,并导致闪烁噪声特性出现变化和改变噪声指数性能直到0Hz。
VSA噪声校正
为了单独地获取解调器和基带VGA的噪声指数,有必要校正由测试设置产生的附加噪声。然而噪声分析主要受分析仪的灵敏度而非源端SNR的影响,因此有必要对分析仪的噪声影响单独进行适当校正。为了测量该VSA的影响,解调器采用强信号电平以确保基带VGA输出端处的SNR达到最佳。这与适用于该DUT的约-50dBm的平均输入电平相一致。
在DUT之后,VSA被插入20 dB衰减器以将信号电平降至略微埋入VSA噪声基底中,这就可以度量VSA对SNR所产生的影响。基于通过DUT的信号增益、测量到的SNR和所施加的输入电平,我们可以计算出分析仪的有效噪声密度。当施加-53dBm输入信号时,对应的EVM分贝值为20dB。
这与α因子为0.35的整形滤波器在1MHz调制带宽时使用500μV均方根输入电压的情形一致。这个包括多种频率的电压是结合1.35MHz分析带宽和431 nV/ Hz源信号密度的结果。解调器和基带放大器的总增益达到了25 dB,而由于施加了输出衰减器,其后将会有约20 dB的衰减。
因此加到I/Q输入端口的信号强度比加到解调器输入的电平大约高5dB,也因此致使EVM值为20dB。请注意,没有衰减器时的EVM性能要好得多,这说明衰减器的确是将信号电平降低到了足以使VSA输入灵敏度对系统起主导限制作用的程度了。该测量说明,VSA输入的噪声密度必须低于所加信号密度20dB以上。建议的VSA输入为~77 nV/ Hz。
总结
结合使用图4中的测量数据和计算得到的VSA输入噪声,就有可能计算出DUT的有效噪声指数。在没有强干扰条件下对有用信号的输入功率进行扫描,输入电平为-71 dBm时,对应的EVM值约为20dB。这是在1.35 MHz分析带宽上测量所得的结果。通过这种测量方法,我们可以预测出-91dBm输入电平对应的SNR为0dB,建议使用-152.3dBm/Hz的输入功率密度。
输入到50Ω的阻抗时,电压密度为5.4nV/Hz。该噪声的一部分是由于VSA噪声引起的。而VSA引起的输入参考噪声则为4.3nV/ Hz。如果我们记住总噪声电平是DUT噪声与测试设备噪声的矢量和,就能够发现来自DUT的噪声为3.3 nV/ Hz。而对于50Ω阻抗,噪声指数为17.3dB。相同的计算方法也用在了零中频和5MHz低中频测试条件下存在强干扰和没有强干扰的情况中。
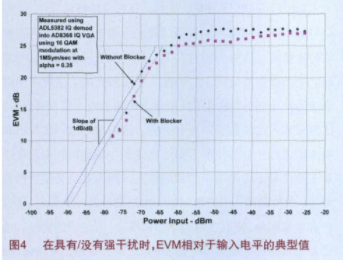
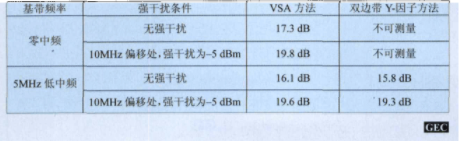
表1对比了VSA测量方法与传统Y-因子测量方法的测量性能。值得注意的是,Y-因子测量方法不适用于零中频情况,因为其所用的测试设备不能在0 Hz提供足够的灵敏度。通过比较证明了VSA测试方法是一种面向基带解调器噪声指数评估的合适的定性解决方案。对于测试台和调试来说,这是一个非常有用的测试工具。不过,当信号电平较小时,其测量方差显得过大,不适合用来对产品特性进行定量。
编辑:jq
全部0条评论

快来发表一下你的评论吧 !
