

K-means 算法是典型的基于距离的聚类算法,采用距离作为相似性的评价指标,两个对象的距离越近,其相似度就越大。而簇是由距离靠近的对象组成的,因此算法目的是得到紧凑并且独立的簇。
假设要将对象分成 k 个簇,算法过程如下:
(1) 随机选取任意 k 个对象作为初始聚类的中心(质心,Centroid),初始代表每一个簇;
(2) 对数据集中剩余的每个对象根据它们与各个簇中心的距离将每个对象重新赋给最近的簇;
(3) 重新计算已经得到的各个簇的质心;
(4) 迭代步骤(2)-(3)直至新的质心与原来的质心相等或小于设定的阈值,算法结束。
注意!
(1) 在 K-means 算法 k 值通常取决于人的主观经验;
(2) 距离公式常用欧氏距离和余弦相似度公式,前者是根据位置坐标直接计算的,主要体现个体数值特征的差异,而后者更多体现了方向上的差异而不是位置上的,cosθ越接近 1 个体越相似,可以修正不同度量标准不统一的问题;
(3) K-means 算法获得的是局部最优解,在算法中,初始聚类中心常常是随机选择的,一旦初始值选择的不好,可能无法得到有效的聚类结果。
对于一堆数据,K 值(簇数)的最优解如何确定呢?常见的有“肘”方法
(Elbow method)和轮廓系数法(Silhouette Coeffient):
① “肘”方法:核心指标是 SSE(sum of the squared errors,误差平方和),即所有样本的聚类误差(累计每个簇中样本到质心距离的平方和),随着 K 的增大每个簇聚合度会增强,SSE 下降幅度会增大,随着 K 值继续增大 SSE 的下降幅度会减少并趋于平缓,SSE 和 K 值的关系图会呈现成一个手肘的形状,此肘部对应的 K 值就是最佳的聚类数。
② 轮廓系数法:结合聚类的凝聚度(Cohesion)和分离度(Separation)来考虑,凝聚度为样本与同簇其他样本的平均距离,分离度为样本与最近簇中所有样本的平均距离,该值处于-1~1 之间,值越大表示聚类效果越好。
以 iris 数据为例:
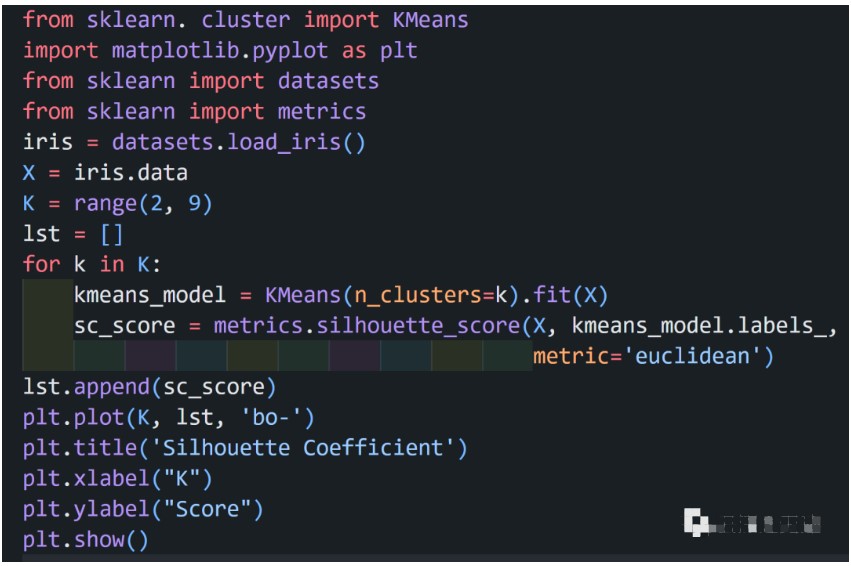
代码实现
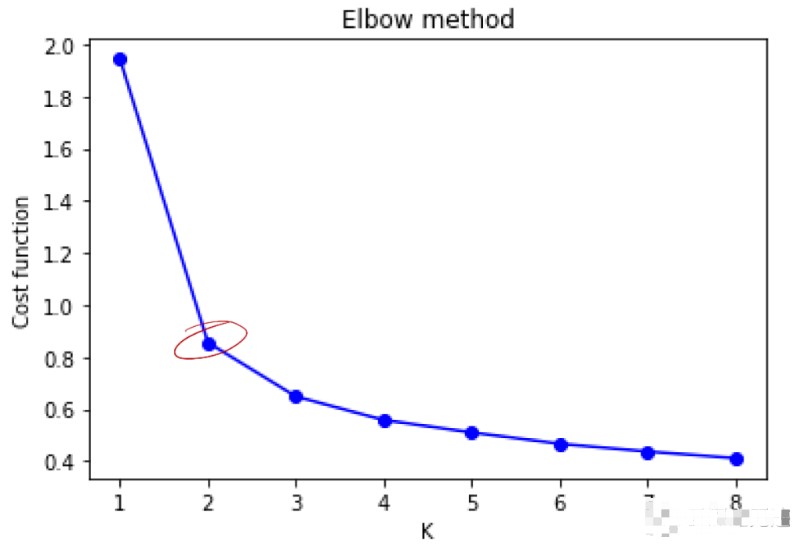
由图看出拐点在 K=2 处,K=3 次之,iris 实际数据分成了三类。
全部0条评论

快来发表一下你的评论吧 !
