Buck电源工作原理详解

Buck电源拓扑结构如图1所示，电压和电流极性如图2所示。Buck电源工作原理如下：1.开关管SW开通时，二极管D反向偏置而截止，二极管电流ID=0，输入电压经过电感给负载RL供电，同时电感和电容储能，电感电流IL逐渐增大，如图1中蓝色环路所示；2.开关管SW关断时，开关管电流IT=0，电感由于自身的自感电动势，通过二极管D续流，继续给负载RL供电，电感电流IL逐渐减小，如图1中红色环路所示。工作过程中，开关管以很高的频率（一般为几十KHz到MHz的量级）不断地重复开通和关断。

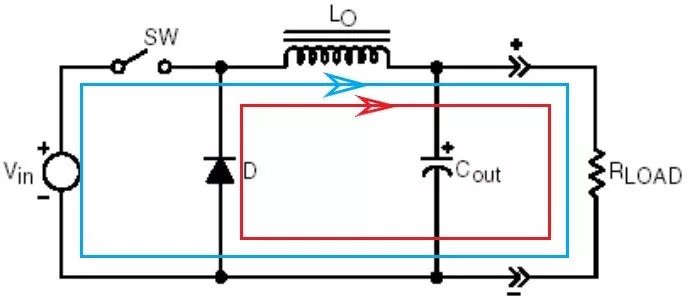
图1

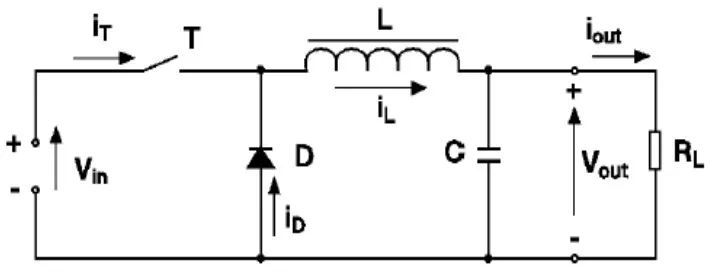
图2

根据能量守恒，在稳态条件下，电感两端电压在一个开关周期内的平均值为0，即伏秒平衡原理。根据电感电流在一个开关周期内是否连续，有三种工作模式，分别是CCM连续电流模式，BCM临界电流模式和DCM不连续电流模式，如图3所示。

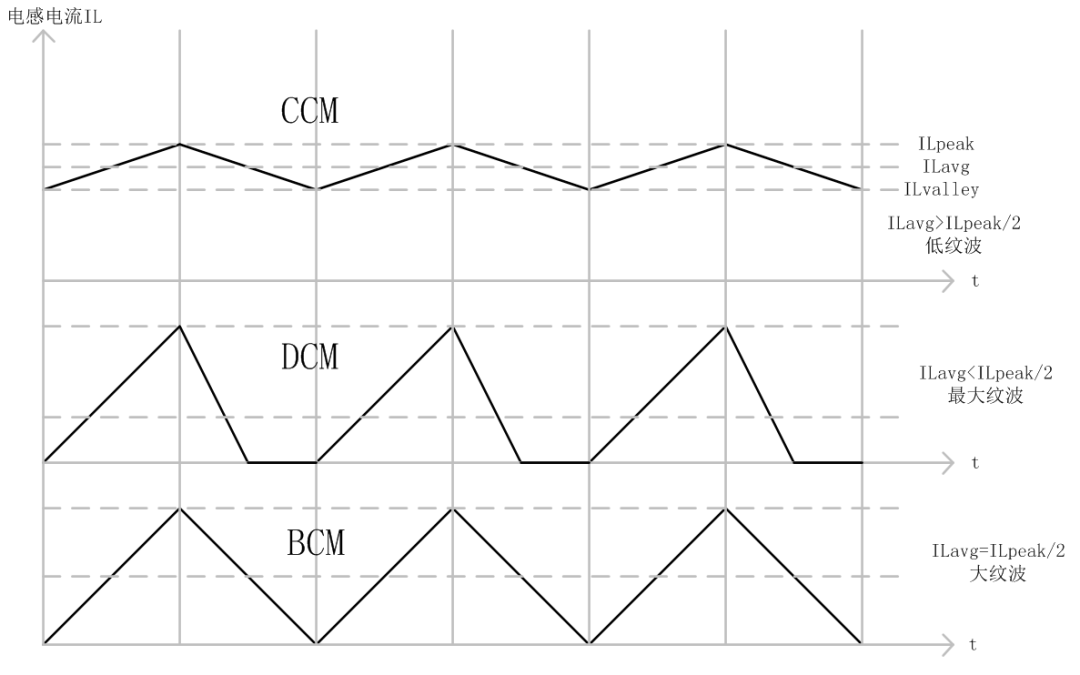
图3

1. CCM连续电流模式

根据伏秒平衡原理，CCM模式在稳态情况下，开通周期D*T内，电感电压为（Vin-Vout）；关断周期（1-D）*T内，电感电压为Vout，前后两者乘积相等，即：

（Vin-Vout）DT=Vout（1-D）T，

其中，D为占空比，T为开关周期，Vin为输入电压，Vout为输出电压，可以得到：

Vout/Vin=D。

由此可见CCM模式下传递函数等于占空比，且和负载电流无关。

CCM模式下的各波形如图4所示，从中可知电感电流不会为0。在开关管SW导通期间，开关管电流IT从某个不为0的值开始上升，直到SW关断时达到最大值。根据公式U=L*dI/dt可得，电流变化率dI/dt=U/L，因此SW导通期间内的电流变化率为（Vin-Vout）/L，在此期间二极管电流ID为0；在开关管SW关断期间，二极管电流ID开始下降，直到SW重新导通时达到最小值，同理可得电流变化率为Vout/L，在此期间开关管电流为0。在整个开关导通和关断的周期内，开关管电流IT和二极管电流ID组合起来就是电感的电流IL。

在开关管SW导通期间，SW点的电压等于输入电压Vin；在开关管SW关断期间为0（忽略二极管和开关管的压降）。开关管SW导通期间，电感左端为输入电压Vin，电感右端为输出电压Vout，因此电感两端电压为（Vin-Vout）；在开关管SW关断期间，电感左端电压为0，右端为输出电压Vout，电感两端电压为（-Vout）。

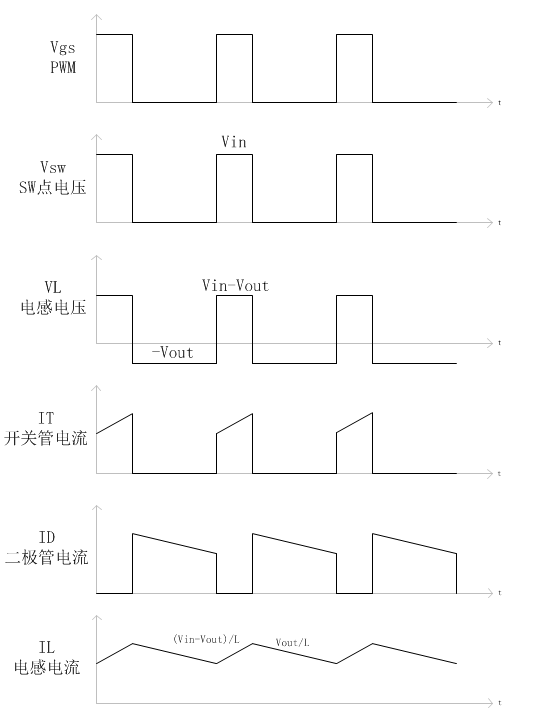
图4

以一个12V转5V的Buck电路为例，测量得到SW引脚的电压波形，如图5所示，可以发现在开关管闭合和断开时，SW处都有一个很大的尖峰，对应的电流波形也会有类似的情况，对图中红圈处的尖峰展开可以发现伴有振荡现象，如图6和图7所示。这是由于二极管或者同步管的寄生电容，以及电路的寄生电感共同造成，**寄生电感不能瞬变的电流对电容进行充电造成电压尖峰和电流尖峰，而振荡是由于电感电容LC谐振造成的。**因此，一般会在二极管或者同步管两端并联一个RC吸收电路来解决这个问题。TI的LM25116芯片建议的RC吸收电路的电阻取值在5~50R之间，电容取几个nf级别。

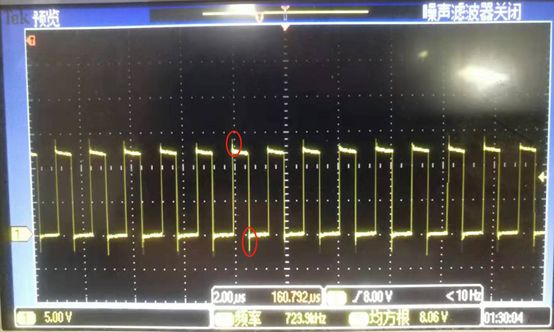
图5

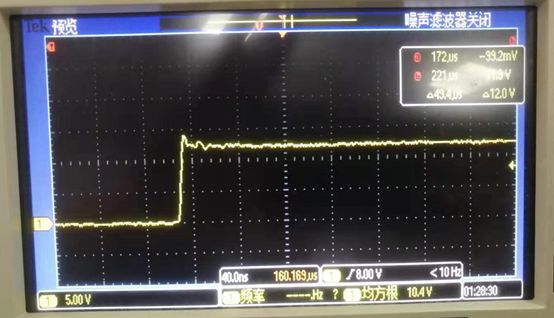
图6

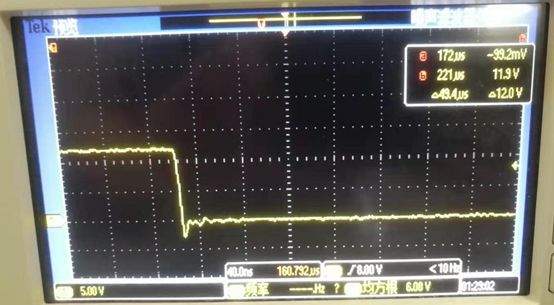
图7

2. DCM不连续电流模式

随着负载电流不断下降，电感将进入DCM模式，此时传递函数、电流和电压波形将发生很大变化，该模式下的输出电流纹波也比CCM模式大。因此要想维持电感在CCM模式下，有最小负载电流值的要求。

稳态情况下，根据伏秒平衡原理有：

（Vin-Vout）D1T=VoutD2T，得：

Vout/Vin=D1/(D1+D2)。

开关管导通，二极管截止的时间长度为D1T；开关管截止，二极管导通的时间长度为D2T；开关管和二极管都截止的时间长长度为（1-D1-D2）*T，D2与电路参数有关。DCM模式下的各波形如图8所示，从图中可知电感电流在某段时间内为0，此时负载电流由电容负责提供。

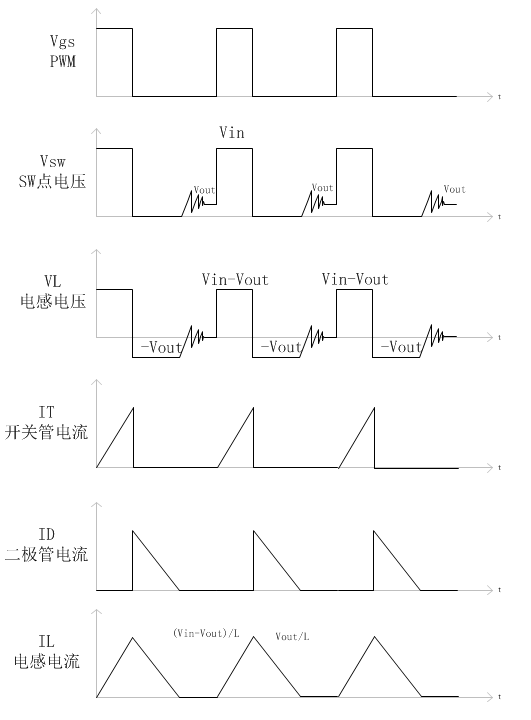
图8

从图中可以发现电感电压存在振荡现象，振荡时间长短与电阻阻尼有关。下面分析原因。从电感电流波形可以看出，当电流下降到0时，续流二极管截止，此时电感左端开路。理论上，电感没有电流通过时，电感左右两端电压应该相等，即电感左端电压也应该等于Vout。但实际上由于续流二极管两端存在寄生电容，还有电阻的存在，因此相当于和恒压源Vout一起形成了RLC串联阻尼谐振。为何CCM模式不会产生振荡，因为电感电流不会下降到0，一直维持固定的电流方向，而LC谐振时充放电电流方向需要反复变化，该条件无法满足，因此不会发生LC谐振。实际测试到LV2843芯片的DCM模式下SW点的电压波形如图9所示，该电路由于设计时电感偏小，因此振荡较强。振荡波形的时间长度随电感值的增大可以在某种程度上相应减小。负载电流越小，电感越小，就越容易进入DCM工作模式。

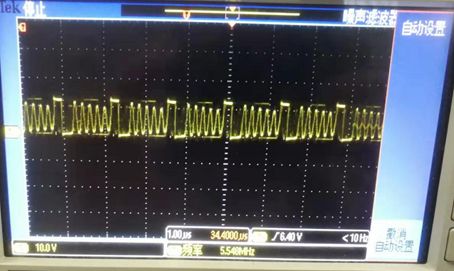
图9

虽然Buck电路在DCM模式下也保持了输出电压恒定不变，但是电路状态和CCM模式相比却不同。在CCM模式下，输出电压Vout=Vin*D，与负载电流无关，即使负载发生变化，占空比也不会改变。在DCM模式下，根据小信号模型可以得到传递函数如下式所示，R为负载。根据该公式可以看出，开关管的占空比D将随着负载电流的减小而减小。

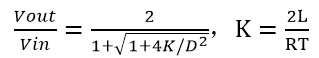
这个公式并不需要我们去记忆，只是帮助我们更好地理解DCM模式下的电路工作状态。