

尽管许多关于调制的描述将其描述为乘法过程,但事实要复杂一些。
首先,要非常清楚,如果一个完美乘法器的两个输入馈送一个信号Acos(ωt)和一个未调制的载波cos(ωt),我们将有一个调制器。发生这种情况是因为两个周期波形 Ascos(ωct) 和 Accos(ωct),应用于乘法器的输入(为简化分析,比例因子为 1 V),产生由下式给出的输出:
Vo(t) = ½AsAc[cos((ωs + ωc)t) + cos(ωs – ωc)t))]
如果承运人,Accos(ωct),具有 1 V 幅度 (Ac= 1),这进一步简化为:
Vo(t) = ½As[cos((ωs + ωc)t) + cos((ωs – ωc)t)]
但是,在大多数情况下,调制器是执行此功能的更好电路。调制器(用作变频器时也称为混频器)与乘法器密切相关。乘法器的输出是其输入的瞬时乘积。调制器的输出是信号在其一个输入(称为信号输入)上的瞬时乘积,在另一个输入(称为载波输入)上是信号的符号。图1显示了调制函数的两种建模方法:作为放大器,其增益由载波输入上的比较器输出切换为正负,或者作为载波输入与其端口之一之间具有高增益限制放大器的乘法器。这两种架构都用于生产调制器,但开关放大器版本(用于AD630平衡调制器)往往较慢。大多数高速集成电路调制器由跨线性乘法器(基于吉尔伯特单元)组成,载波路径中的限幅放大器用于过驱动其中一个输入。该限幅放大器可以提供高增益,允许低电平载波输入,或低增益和干净的限幅特性,因此需要相对较大的载波输入才能正常工作。有关具体信息,请参阅数据手册。
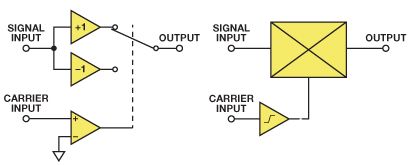
图1.调制函数建模的两种方法。
我们使用调制器而不是乘法器有几个原因。乘法器的两个端口都是线性的,因此载波输入上的任何噪声或调制都会使信号输入成倍并降低输出,而调制器载波输入的幅度变化大多可以忽略不计。二阶机制会导致载波输入端的幅度噪声影响输出,但在最好的调制器中,这些噪声被最小化,这里不讨论。调制器的简单模型使用由载波驱动的开关。(完美)开路开关具有无限电阻和零热噪声电流,而(完美)闭合开关具有零电阻和零热噪声电压,因此调制器即使开关不完美,内部噪声也往往低于乘法器。此外,与类似的乘法器相比,设计和制造高性能、高频调制器更容易。
与模拟乘法器一样,调制器将两个信号相乘,但与模拟乘法器不同,乘法不是线性的。相反,当载波输入的极性为正时,信号输入乘以+1,当极性为负时乘以-1。换句话说,信号乘以载波频率的方波。
频率为 ω 的方波ct可以用奇次谐波的傅里叶级数表示:
K[cos(ωct) – 1/3cos(3ωct) + 1/5cos(5ωct) – 1/7cos(7ωct) + …]
序列的总和: [+1, –1/3, +1/5, –1/7 + ...] 为 π/4。因此,K的值为4/π,这样当正直流信号施加到其载波输入时,平衡调制器充当单位增益放大器。
载波幅度只要足够大以驱动限幅放大器就不重要,因此由信号驱动的调制器As余弦(ωst)和一个载波cos(ωct),将产生信号和平方载波的乘积:
2As/π[cos(ωs + ωc)t + cos(ωs – ωc)t –
1/3{cos(ωs + 3ωc)t + cos(ωs – 3ωc)t} +
1/5{cos(ωs + 5ωc)t + cos(ωs – 5ωc)t} –
1/7{cos(ωs + 7ωc)t + cos(ωs – 7ωc)t} + …]
该输出包含信号和载波的和差频率,以及信号和载波的每个奇次谐波的和和差。在理想、完美平衡的调制器中,不存在偶次谐波的产物。然而,在实际调制器中,载波端口上的残余偏移会导致低电平、均匀的谐波产物。在许多应用中,低通滤波器(LPF)可去除高次谐波的产物。请记住,cos(A) = cos(–A),所以 cos(ωm– Nωc)t = cos(Nωc– ωm)t,我们不必担心“负”频率。滤波后,调制器输出由下式给出:
2As/π[cos(ωs + ωc)t + cos(ωs – ωc)t]
这与乘法器的输出表达式相同,只是增益略有不同。在实际系统中,增益由放大器或衰减器归一化,因此我们不会在这里考虑各种系统的理论增益。
在简单的情况下,使用调制器显然比乘法器更好,但是我们如何定义简单?当调制器用作混频器时,信号和载波输入是频率f的简单正弦波1和 fc,并且未过滤的输出包含总和 (f1 + fc) 和差异 (f1– f c) 频率,加上信号的和差频率以及载波的奇次谐波 (f1 + 3fc), (f1 – 3fc), (f1 + 5fc), (f1 – 5fc), (f1 + 7fc), (f1 – 7fc)… 在LPF之后,我们希望只找到基本面产品,(f1 +fc) 和 (f1–fc).
如果 (f1 + fc) > (f1– 3层c),但是,不可能用简单的LPF分离基波和谐波积,因为其中一个谐波积的频率低于基波积之一的频率。这不是一个简单的案例,因此需要进行更多分析。
如果我们假设信号包含单个频率,f1,或从 f 扩展到整个频段的更复杂的信号1到 f2,我们可以分析调制器的输出频谱,如下图所示。假设调制器完美平衡,没有信号泄漏、载波泄漏或失真,因此输入、载波和杂散产物不会出现在输出中。输入以黑色显示(或在输出图中以浅灰色显示,即使它实际上并不存在)。
图2显示了输入 - f中的信号1到 f2波段和 F 处的载波c.乘法器在 1/3(3f 处不会有奇数载波谐波c), 1/5(5Fc), 1/7(7层)c)...,显示为调制器的虚线。请注意,分数 1/3、1/5 和 1/7 是指振幅,而不是频率。
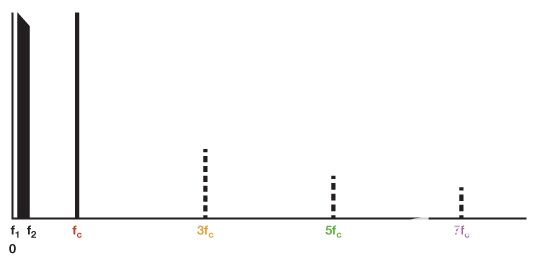
图2.输入频谱显示信号输入、载波和奇数载波谐波。
图3显示了倍频器或调制器的输出,以及截止频率为2f的LPFc.
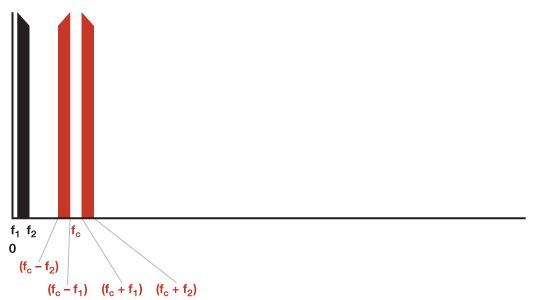
图3.乘法器或调制器的输出频谱加上LPF。
图4显示了未滤波调制器的输出(但不包括高于7f的谐波产物)c).
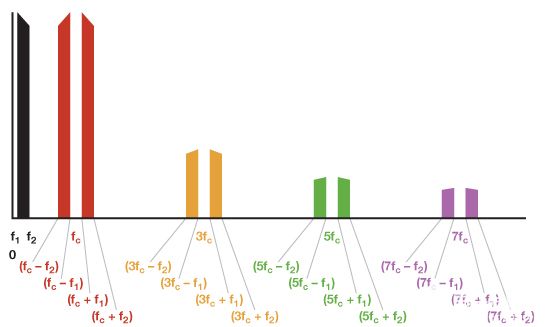
图4.未滤波调制器的输出频谱。
如果信号频段,f1到 f2,位于奈奎斯特带内(dc 到 fc/2),截止值高于 2f 的 LPFc将导致调制器具有与乘法器相同的输出频谱。在信号频率高于奈奎斯特时,事情变得更加复杂。
图5显示了当信号频带略低于f时会发生什么情况c.仍然可以将谐波产物与基波产生的谐波产物分开,但现在它需要具有非常陡峭滚降的LPF。
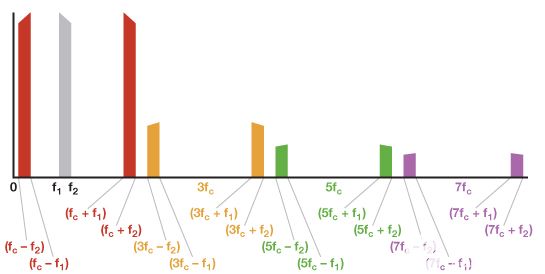
图5.信号大于f时的输出频谱c/2.
图6显示,当信号频带通过fc,谐波积现在重叠(3Fc– f1) < (fc + f1),因此基波积不能再通过LPF与谐波积分离。现在必须通过带通滤波器(BPF)选择所需的信号。
因此,尽管调制器在大多数频率变化应用中优于线性乘法器,但在设计实际系统时考虑其谐波产物非常重要。
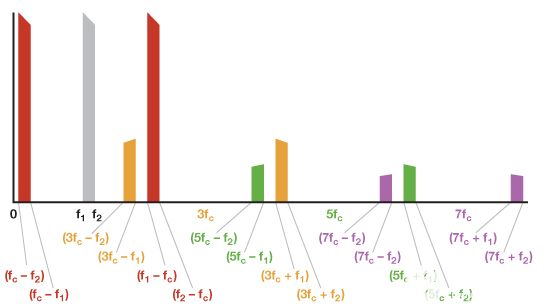
图6.信号超过f时的输出频谱c.
审核编辑:郭婷
全部0条评论

快来发表一下你的评论吧 !
