

模拟技术
在使用卡尔曼滤波器做姿态估计(Attitude Estimation)中,很大一部分都采用不是直接将系统姿态角作为卡尔曼滤波的状态,而是将姿态角的积分误差和角速度计的误差作为系统状态。
将角速度计的输出弥补上估计出的角速度计误差,然后对其积分,得到姿态角的估计,再弥补上姿态角的误差估计。整个的流程图大概如下面的图,引用自Intertial Head-Tracker Sensor Fusion by a Complementary Separate-Bias Kalman Filter
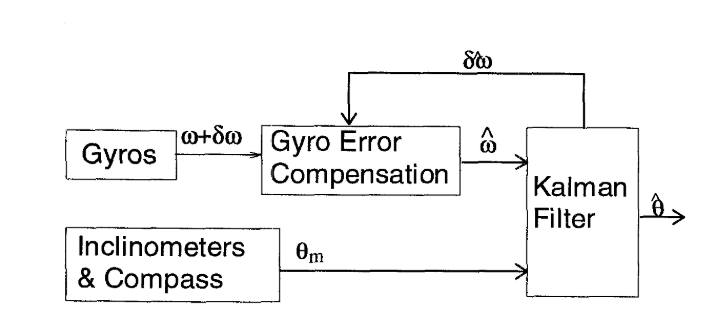
PS: 要强调的是,各种卡尔曼滤波的形式多种多样,同时各种符号的定义也都并不完全一致,这也是入门卡尔曼滤波比较难的地方,有时候找资料都不知道怎么找。这也是写这篇文章的目的,提供一个基础的脉络给卡尔曼滤波的初学者。因此这里给出的ErKF只是形式之一,主要是引用自论文Extended Kalman Filter vs. Error State Kalman Filter for Aircraft Attitude Estimation
首先,我们令表示时间连续形式的状态向量。其相对于时间的导数为
在等号的右边输入里加入微小扰动,同时,根据泰勒展开将函数展开

则
将上式使用离散形式表达
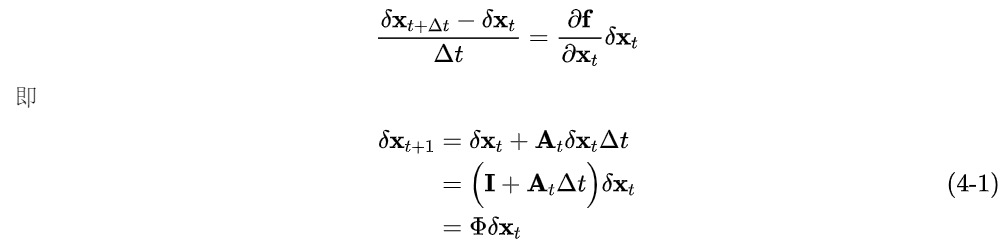
于是,有了状态误差的递推公式,我们就可以像卡尔曼滤波一样推导预测和更新过程
与直接对系统状态做卡尔曼滤波稍有不同,使用误差状态的卡尔曼滤波在计算姿态角的时候可以看成三步:
上式只是一个公式化表达,其实就是将上一时刻的状态,在加上这一时间段状态的变化量。姿态估计中,状态的变化量通常是角速度计的输出乘以时间间隔。
状态误差方程
由公式(4-1)可以得到状态误差的方程为

其中,是过程噪声,协方差矩阵为
预测方程
类似于普通卡尔曼滤波,预测方程为

这里我们直接将使用其余传感器如加速度计、磁力计计算出的姿态作为系统的测量量。在这里先记得,加速度计根据输出的夹角可以计算出角,由磁力计可以计算出角即可。当然,也可以采用其他能够直接输出系统姿态角的传感器作为测量值。
测量方程
其中,是测量噪声,协方差矩阵为
更新方程
这里要执行两步更新
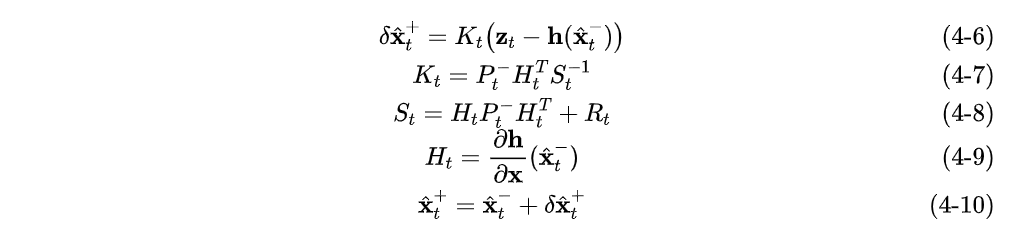
在上面的推导中,将我们的目标变量,即系统的姿态角作为外部一个单独的积分计算,但是实际上更多的做法是将姿态角和角速度的偏差直接放在状态向量中进行计算。然后对每一时刻的角速度偏差应用到角速度计的输出,再将其作为系统输入应用到状态方程。
也就是像概述中的图示那样。但是其实各种卡尔曼滤波的建模方式都不一样,Error-state Kalman Filter和Complimentarty Kalman Filter也没有严格的定义。所以索性这一章节当作对状态误差的理解和推导,在下面的互补卡尔曼滤波给出一种似乎是应用更广泛的卡尔曼滤波器。
全部0条评论

快来发表一下你的评论吧 !
