

阻抗匹配,作为射频设计中最为重要的一个环节,每一个射频工程师都无法绕过去的。 今天我们再加以总结,把整个阻抗匹配,展现给大家。
阻抗三兄弟
射频工程师必知必会—— 阻抗,特征阻抗与等效阻抗
阻抗,顾名思义就是对电路中电流起到阻碍作用的元器件。 我们在射频电路中,又引入了特征阻抗和等效阻抗两个概念。
No.1.1 阻抗
谈到阻抗的概念,大家的第一影响就是电阻和电抗的组合。 没错,在低频领域,或者在我们学习的电路原理的课程中,阻抗就是电阻和电抗的组合。
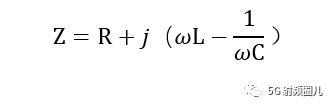
我们借用百度百科的定义就是:
在具有电阻、电感和电容的电路里,对电路中的电流所起的阻碍作用叫做阻抗。 阻抗常用Z表示,是一个复数,实部称为电阻,虚部称为电抗,其中电容在电路中对交流电所起的阻碍作用称为容抗 ,电感在电路中对交流电所起的阻碍作用称为感抗,电容和电感在电路中对交流电引起的阻碍作用总称为电抗。 阻抗的单位是欧姆。
阻抗可以是电阻、电容、电感的任意组合对电流起到的阻碍作用。 由于电容对直流电的阻抗无穷大,而电感对直流电的阻抗是零,因此,阻抗更多用于描述交流电路中对电流的阻碍作用。 高阻抗是指阻抗值大,低阻抗是指阻抗值小。
对于一个具体电路,阻抗不是不变的,而是随着频率变化而变化。 在电阻、电感和电容串联电路中,电路的阻抗一般来说比电阻大。 也就是阻抗减小到最小值。 在电感和电容并联电路中,谐振的时候阻抗增加到最大值,这和串联电路相反。
阻抗从字面上看就与电阻不一样,其中只有一个阻字是相同的,而另一个抗字呢? 简单地说,阻抗就是电阻加电抗,所以才叫阻抗; 周延一点地说,阻抗就是电阻、电容抗及电感抗在向量上的和。 在直流电的世界中,物体对电流阻碍的作用叫做电阻,世界上所有的物质都有电阻,只是电阻值的大小差异而已。 电阻小的物质称作良导体,电阻很大的物质称作非导体,而最近在高科技领域中称的超导体,则是一种电阻值几近于零的东西。
但是在交流电的领域中则除了电阻会阻碍电流以外,电容及电感也会阻碍电流的流动,这种作用就称之为电抗,意即抵抗电流的作用。 电容及电感的电抗分别称作电容抗及电感抗,简称容抗及感抗。 它们的计量单位与电阻一样是奥姆,而其值的大小则和交流电的频率有关系,频率愈高则容抗愈小感抗愈大,频率愈低则容抗愈大而感抗愈小。 此外电容抗和电感抗还有相位角度的问题,具有向量上的关系式,因此才会说:阻抗是电阻与电抗在向量上的和。
阻抗匹配是指负载阻抗与激励源内部阻抗互相适配,得到最大功率输出的一种工作状态。 对于不同特性的电路,匹配条件是不一样的。 在纯电阻电路中,当负载电阻等于激励源内阻时,则输出功率为最大,这种工作状态称为匹配,否则称为失配。
当激励源内阻抗和负载阻抗含有电抗成份时,为使负载得到最大功率,负载阻抗与内阻必须满足共扼关系,即电阻成份相等,电抗成份只数值相等而符号相反。 这种匹配条件称为共扼匹配。
No1.2 特征阻抗
特征阻抗是射频传输线的一个固有特性,其物理意义是在射频传输线上入射波电压与入射波电流的比值,或者反射波电压和反射波电流的比值。
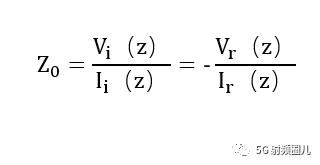
如果按照分布参数的理论去表示,传输线的特征阻抗可以表示为:
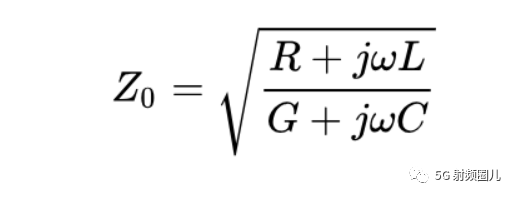
从上式可以看出,对于一个有耗传输线来说,特征阻抗是一个复数,有耗传输线的损耗就来自于这个传输线的电阻。 而对于理想的无耗传输线来说,特征阻抗就是一个实数。 这也就告诉我们,对于一个理想的无耗的50欧姆传输线来说,其电阻为0,这和上文中的带电阻的阻抗就不一样了。
特性阻抗是射频传输线影响无线电波电压、电流的幅值和相位变化的固有特性,等于各处的电压与电流的比值,用V/I表示。 在射频电路中,电阻、电容、电感都会阻碍交变电流的流动,合称阻抗。 电阻是吸收电磁能量的,理想电容和电感不消耗电磁能量。 阻抗合起来影响无线电波电压、电流的幅值和相位。 同轴电缆的特性阻抗和导体内、外直径大小及导体间介质的介电常数有关,而与工作频率传输线所接的射频器件以及传输线长短无关。 也就是说,射频传输线各处的电压和电流的比值是一定的,特征阻抗是不变的。 对于一个已知特性阻抗的传输线来说,它与频率无关。
相关阅读,可参考长线理论:射频工程师必知必会——长线效应与分布参数
No1.3 等效阻抗
等效阻抗也是传输线理论的一个概念,我们在设计中,经常要求知道在传输线上指定位置的阻抗是多少。 这个指定位置的阻抗就是等效阻抗Z(z),其定义为传输线上该位置处的电压和电流的比值:
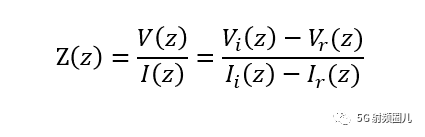
注意对比特征阻抗与等效阻抗定义公式之间的区别:特征阻抗是入射波或者反射波的比值,而等效阻抗则是指定位置处入射波和反射波两者叠加之后的比值。 这个是位置的函数。 对于无耗传输线来说,特征阻抗是固定的,而等效阻抗则随位置的不同而变化。
这个位置的变化,还涉及到一个看过去的方向问题。 比如我们看向负载还是源,这个所得到的等效阻抗,有时候是有区别的。 我们设定观察点,向负载看去的等效阻抗,就是负载阻抗。
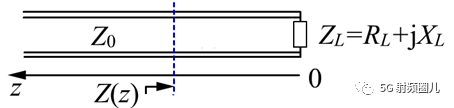
如上图所示,如果我们在指定的位置z处截断,在负载处用一个阻抗为Z(z)的来代替系统中的负载部分,那么对于截断点到电源部分的电压和电流分布将不会改变,这说明Z(z)与截断的电路ZL相等,Z(z)就是负载的等效阻抗,或称为负载阻抗。
相反,如果我们向源的方向看去,我们把源到截断点的阻抗用Z(z)来替代Zin,那么从截断点到负载的传输特性也不会改变,那么这个Z(z)就可以表示为系统的输入阻抗。

等效阻抗与特征阻抗的关系可以用反射系数来计算。
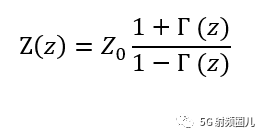
只要知道传输线上指定位置的反射系数,就可以得到其等效阻抗。 相应的,如果知道传输线上的等效阻抗,就可以求出该位置的反射系数。
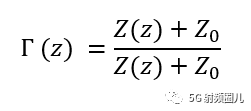
我们如果用传输线上的电流和电压方程来表示等效阻抗Z(z)的话,我们还能够发现一个更有趣的现象。
电流和电压方程:
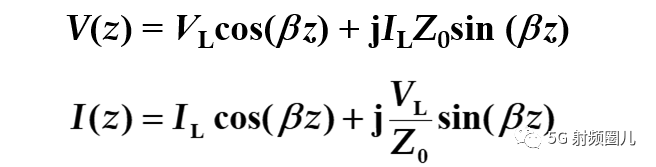
带入等效阻抗方程可得到:
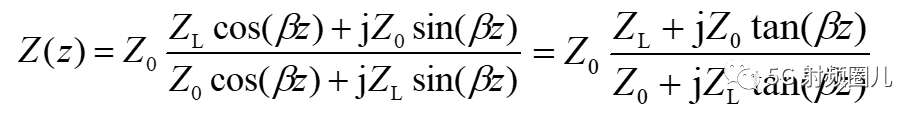
注意观察上述方程,您是否注意到方程里面的那个Tan,也就是说,在无耗传输线上等效阻抗是三角函数的复合函数。 由于三角函数的周期性特征,无耗传输线上的等效阻抗也必然具有周期性。 这个周期就是pi,180°。
至此,我们不难发现,在传输线上,任意相距二分之波长和其整数倍的位置,其等效阻抗相等。
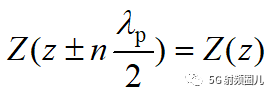
二是在传输线上,任意相距四分之一波长极其整数倍的位置等效阻抗满足如下关系式:
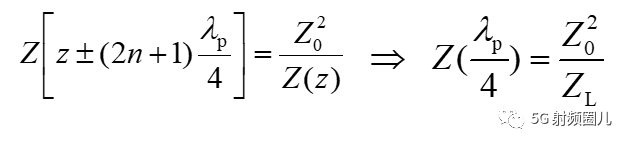
这就巧了,当负载处阻抗等于0时,那么距离负载二分之一波长整数倍的地方阻抗也等于零,在距离负载四分之一波长整数倍的位置等效阻抗则为无穷大。
相反,当负载阻抗为无穷大时,上述结论也翻一下。 这不就是开路短路状态的转化吗? 在射频设计中,会经常用到哦。 您用过没?
为什么要阻抗匹配
阻抗匹配就是为了电磁波能够更好的传播。 我们总是希望有用的射频信号能够无衰减或者小衰减的传输到负载,如果阻抗不匹配的话,反映到系统的就是该器件的回波损耗差。 回波损耗也是损耗。 这个反射回去的射频信号,会对系统造成很大的影响,甚至烧坏某些器件。
什么是回波损耗? 什么是插入损耗?
我们通过例子讲述了回波损耗到底反射回去多少射频功率。
电磁波功率P1 从端口1进入网络,从端口2出来。 由于在端口1处存在不匹配,那么有一部分电磁波功率P1- 反射回去。
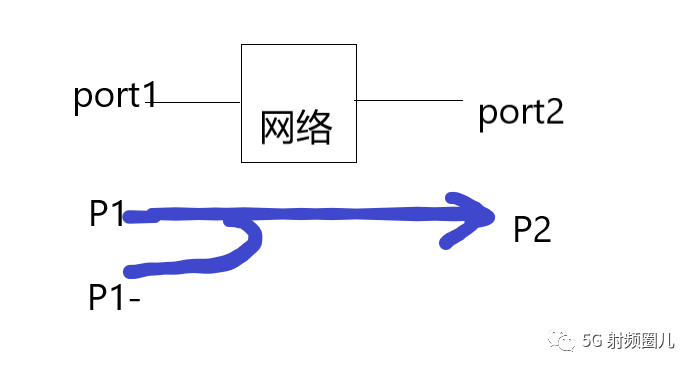
回波功率P1-应该怎么算呢?
对于一个双端口网络,我们只要知道其S2p文件,就可以确定网络的特性,至于网络内部到底是什么样子,我们不用关心,有时候也不需要去关心。
我们再来看一下回波损耗的定义。 回波损耗就是反射损耗,是反射系数的dB形式。
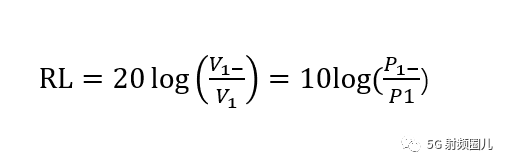
那么问题就转换成了已知输入功率P1和回波损耗RL,求回波的功率P1-。
根据上面公式,直接求,就可以算出来了。 公式如下。
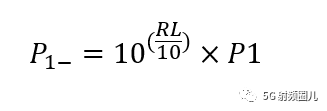
那我们再两边同时取dB呢? 也就是 加上 10log,就成了下面形式。
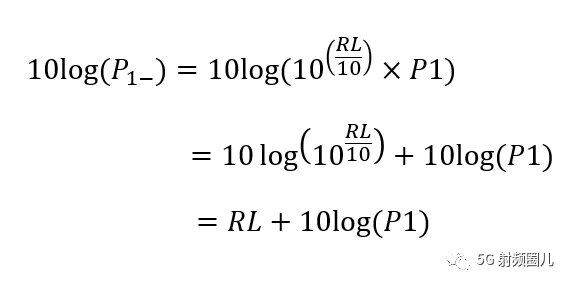
通过上述计算推导,我们得知,回波损耗的功率就是 输入功率P1加上回波损耗RL(注意,RL此处为负值)。 所以对于大功率器件,我们对其回波损耗的要求越严格。 对于小信号器件,有时候可以放宽回波损耗的指标。
共轭匹配和负载匹配
共轭匹配的意义是在于信号源能够输出最大的功率到负载,而负载匹配则是负载能够吸收最大的功率。 这两种都是我们做匹配负载所要做的。
说起共轭匹配,我们先复习一下共轭的概念。
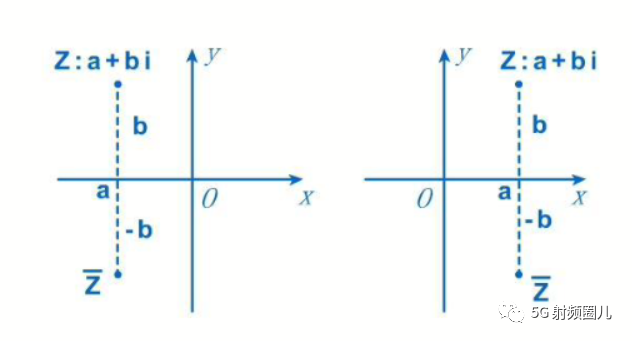
一提到数学就头疼,共轭是什么玩意? 带大家一起回忆一下。 共轭就是两个复数的实部相同,虚部符号相反,大小相等,如下图所示,在复平面上,共轭也就是在坐标系里沿着x轴(实轴)镜像了一下。
实现最大功率传输,为什么要共轭呢? 我们一起看一下。 假设在一个最简单的电路中,如下图所示,Us为信号源电压,Rs为信号源内阻,RL为负载电阻。 在什么情况下才能够使得信号源把最多的功率提供给负载呢? 也就是如何让信号源的输出功率尽可能大。
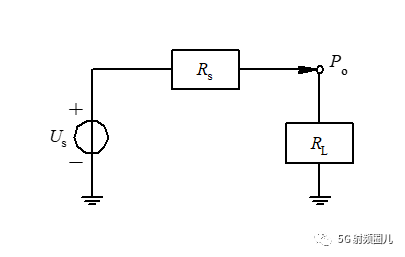
利用上面这个简单的电路,很容易得到信号源输出功率与电路元器件之间的关系:
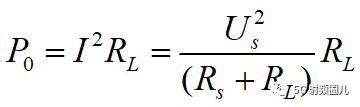
在这里,我们假设:
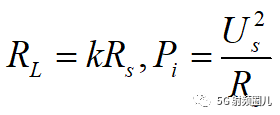
这时,我们就可得到:
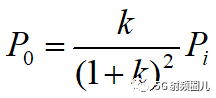
我们就得到了,信号源的输出功率只取决于Us,Rs和RL。 当信号源一定时,输出功率只取决于k,负载阻抗和信号源内阻的比值。
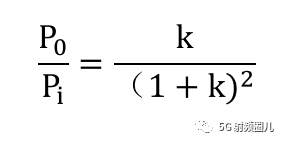
取右边的极值呗。 我们也可以得到这个功率比和阻抗比的关系曲线。
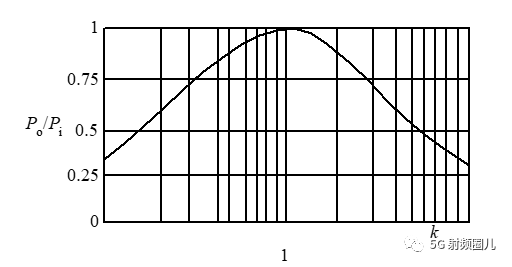
也就是当k等于1时,即RL=Rs时,负载可获得最大的输出功率,此时的状态为匹配状态。 无论负载阻抗大于还是小于信号源内阻,都不可能使得负载获得最大功率,并且这两个电阻值偏差越大,输出功率就越小。
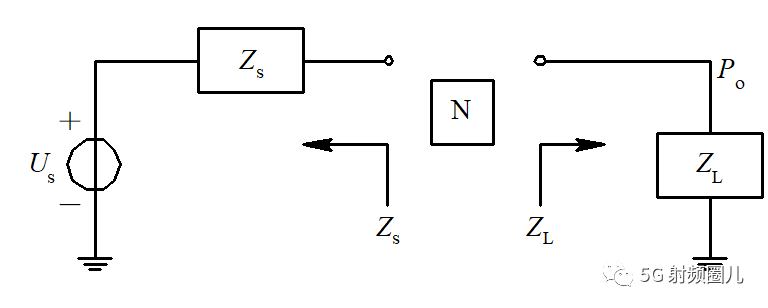
当源阻抗为复数时,我们可以用同样的推导过程进行计算。 这时的等效电路如下图所示:
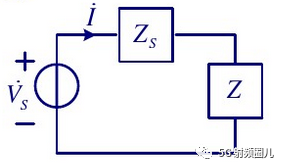
其信号源电压为Vs,信号源内阻为Zs=Rs+jXs。 负载阻抗为Z=R+jX。 电路中的电流为:
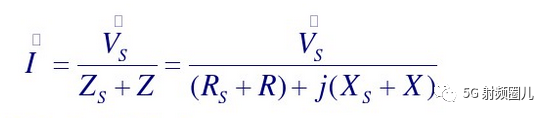
电流的幅度值为:
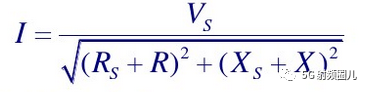
负载处的功率为:
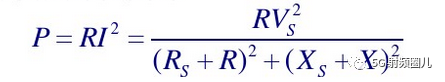
参照前文到的结论,当R=Rs,X=-Xs时,负载的功率最大,即输出功率最大。 这时即有
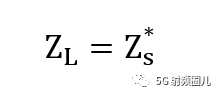
那么在共轭匹配下,负载能够得到最大的功率是多少呢?
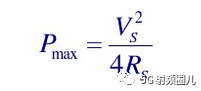
只有四分之一的源功率能够到负载,剩下的到哪去了呢? 被源自己的电阻吃掉了。 所以我们发现,源都是最热的那一个。
如果负载阻抗不能满足共轭匹配条件怎么办呢? 很简单,让他匹配嘛,在源与负载之间加一个匹配网络,将负载阻抗变换为信号源阻抗的共轭匹配。 这个阻抗变换就是阻抗匹配的重要方法之一。
如何进行阻抗匹配?
阻抗匹配的方法有很多,我们在之前的文章中介绍了集总参数阻抗匹配电路和阻抗变换器和短截线分布参数匹配,这其中也详细介绍了Smith Chart的用法。 但是这其中的匹配都是对于单频点的匹配,其大部分匹配都是窄带的。 而宽带匹配电路我们在以后的章节,会详细介绍。
No4.1 集总参数匹配电路
集总参数对应着分布参数,我们知道在低频频段,我们常用的一些电阻电容电感就是集总参数元件。 在微波和微波低端的电路设计中,我们也常用到集总参数的元器件,因此采用集总参数元器件来进行阻抗匹配,也是在射频设计中经常用到的。
常见的集总参数匹配电路有三种,L型,T型和Π型。 我们在这里一一进行学习。
4.1.1 L型匹配电路
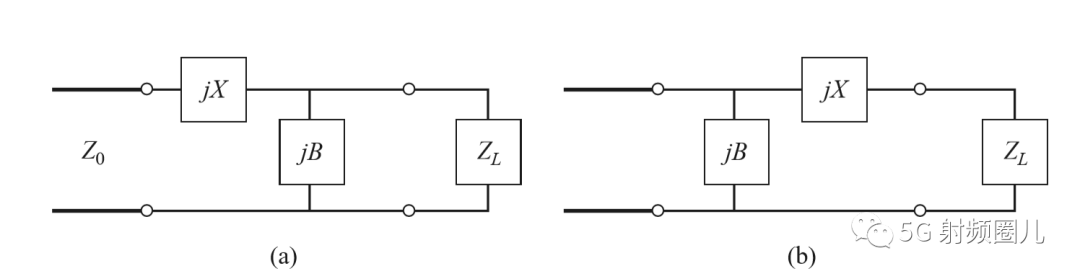
常用的L型匹配电路有两种,如下图所示,即右L(图a)和左L(图b)。 这种匹配电路只有两个元器件,简单易做,成本低廉并且性能稳定。 应用比较广泛。
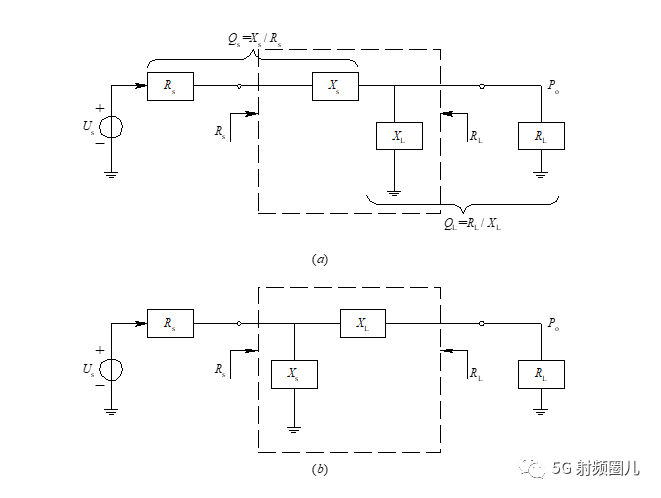
在电路匹配中,左L和右L的选择由所需要匹配的负载阻抗和源阻抗的关系决定。
对于负载阻抗RL和源阻抗Rs 都为纯电阻的情况下,详细过程如下:
1, 确定工作频率fc,源阻抗Rs和负载阻抗RL。 这就是我们对电路匹配左右处理的对象。
2,根据前文所述的共轭匹配条件,可以推导出:
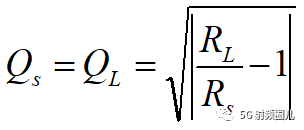
3, 根据源阻抗和负载阻抗的大小关系进行判断,计算:
如果 Rs,则选用右l电路进行匹配:<>
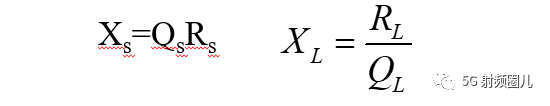
如果 Rs>RL,则选用左L电路进行匹配:
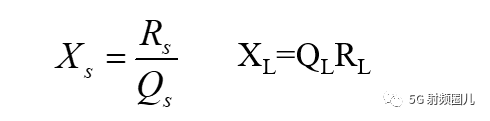
4, 当选出匹配电路形式之后,可利用电感和电容组成的电路进行阻抗匹配。
对于 右L 型电路,可以分为Ls-Cp 低通形式,也可以采用Cs-Lp 高通形式, 如下图所示:
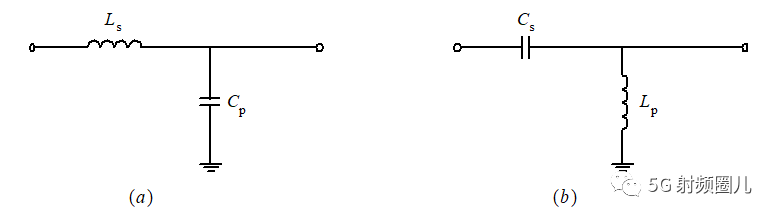
Ls-Cp低通电路,电感和电容值可以有以下公式计算:
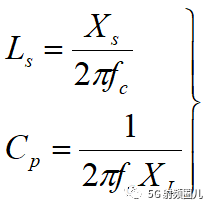
Cs-Lp高通电路,电感和电容值可以有以下公式计算:
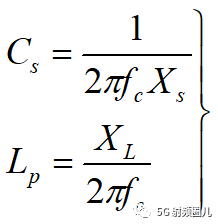
至于高通形式还是低通形式可以根据电路设计的需求进行选择。
同理,如果Rs>RL, 则选用左L型,其电路形式依然可以分为低通型和高通型。

低通电路,电感和电容值计算公式:

高通电路,电感和电容值计算公式:
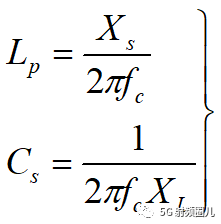
注释,当源阻抗和负载阻抗不是纯电阻时,处理的方法也很简单,只考虑电阻部分,按照上述方法计算中匹配电路中的电容和电感值,再扣除两端的虚数部分,就可得到实际的匹配电路。
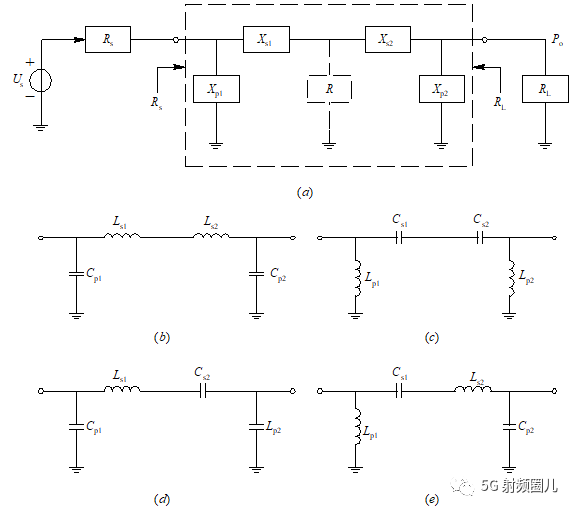
4.1.2 T型匹配电路
T型匹配电路也是一种常见的匹配方法,其一般有三个元件组成,因此复杂度略高于L型。 如下图a所示,其常用的四种形式有图b,c,d,e。
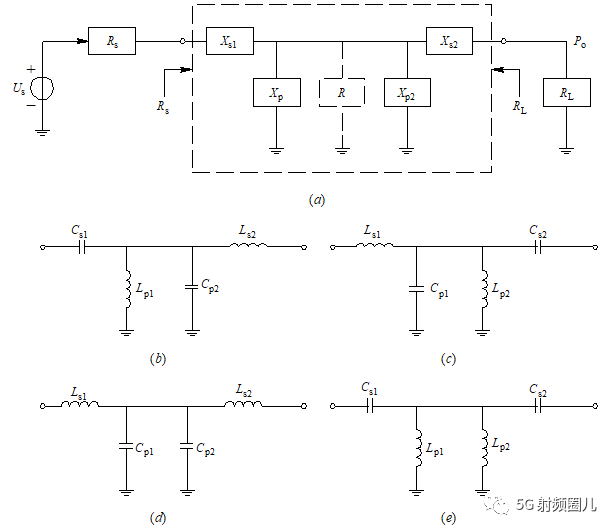
T型匹配电路的分析方法可参照L型匹配电路,我们不再详细说明,其计算公式如下:
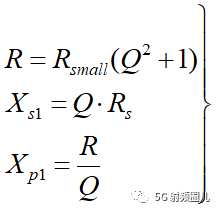
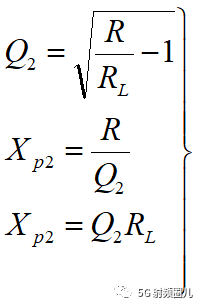
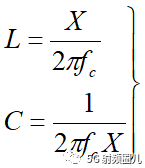
4.1.3 Π型匹配电路
Π型匹配电路的结构如下图a所示,我们这里只根除设计公式。
设计公式:
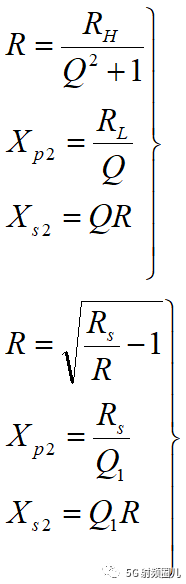
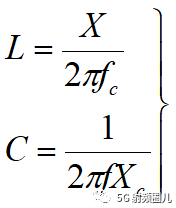
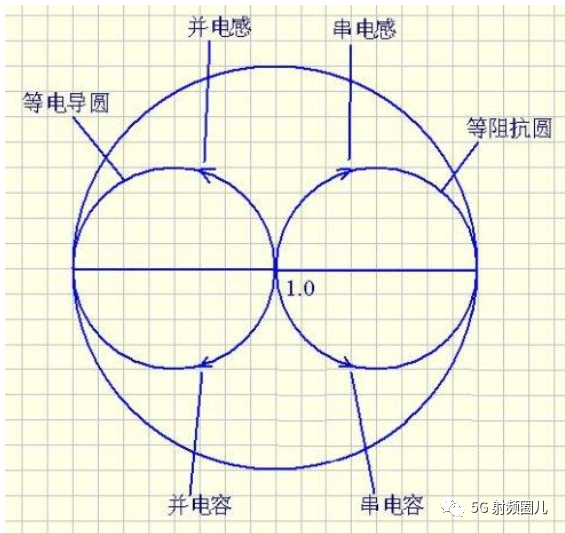
对于电路匹配,有一个重要的工具,就是史密斯圆图,现在很多的射频电路仿真软件上,如ADS和AWR等,都集成有史密斯圆图工具,我们可以利用史密斯圆图,快速得到电路的匹配网络。
No4.2 Smith Chart 匹配示例
问题:
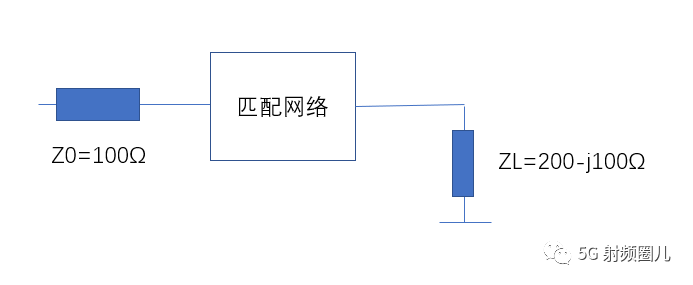
设计一个L型匹配网络,使其在频率500MHz处,完成负载到传输线的匹配。 负载阻抗为ZL=200-j100Ω,传输线阻抗为Z0=100Ω。
这个问题的示意图如下:
常见的L型匹配电路有两种,左L和右L,具体选择哪种,可根据源阻抗与负载阻抗的大小关系来定S(不得不掌握的几种常见的集总参数阻抗匹配电路)。
首先我们将负载阻抗ZL归一化得到zL=2-j,把这个点标注在Smith 圆图上。 这个点在1+jx的圆内部,所以我们选用右L型匹配电路,或者按照我们上节学习到的规律RL>RS(不得不掌握的几种常见的集总参数阻抗匹配电路)。 从负载看过去,第一个元件时并联电纳B,通过负载话SWR圆,且从负载过圆心画一条直线,就可以把负载阻抗转换成导纳,才能与该并联导纳相加。
我们加上这个并联导纳之后再转换回阻抗,将它画在1+jx圆上,这样我们才能加上一个串联电抗来抵消jx并与负载匹配。 也就是说,这个并联电纳B能够将YL转移到Smith圆图的1+jx圆上。 我们可以看到在外加一个jb=j0.3电纳之后,便能沿着等电导圆移动到y=0.4+j0.5处,再将导纳转换成相应的阻抗z=1-j1.2,在此处接上串联电抗x=j1.2就可实现匹配。 使我们回到Smith圆图的中心点。
详细过程如下:
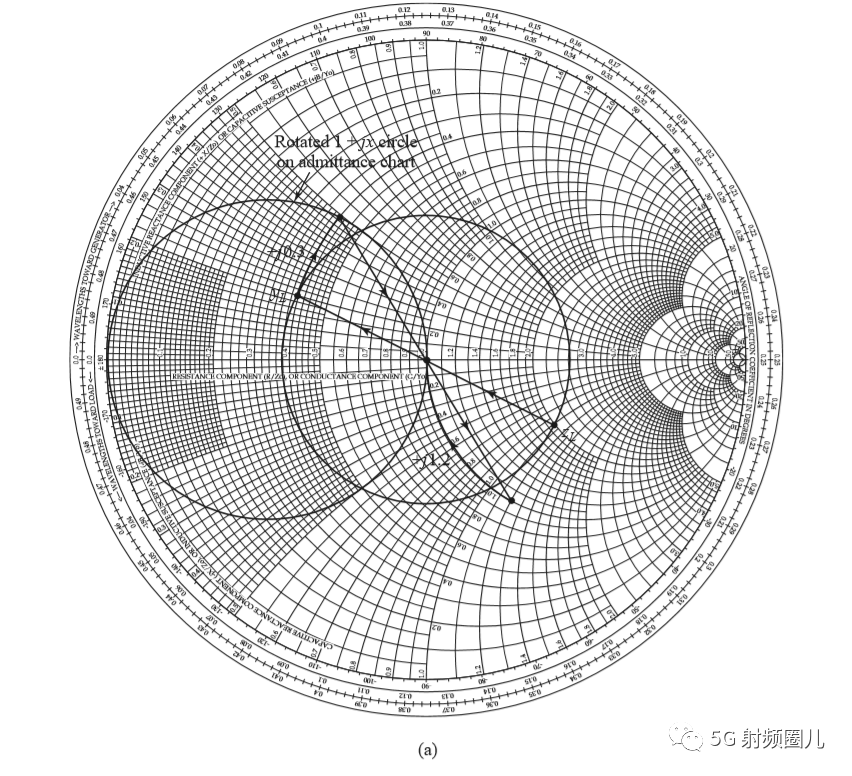
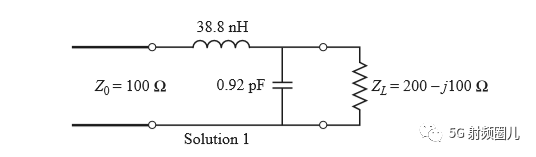
如果该匹配电路是由一个并联电容和串联电感组成,如下图所示,在频率f=500MHz处,可求出该匹配电路的电容值和电感值。
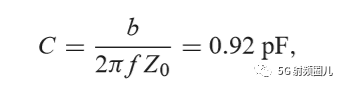
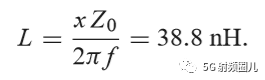
如果我们用一个b=-j0.7的并联电纳来替换之前外加的b=j0.3的并联电纳,则在移位后的1+jx圆的下班圆移动这个点到y=0.4-j0.5处,然后转换回阻抗并且加上一个x=-1,2 的串联电抗,也可以达到匹配。 这时,匹配网络使一个有并联电感和串联电容来实现。 在频率f=500MHz时的电感和电容值可以计算得出:
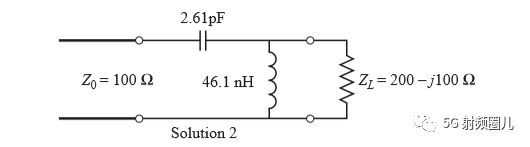
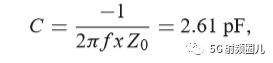
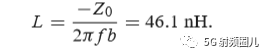
对于这两种匹配网络,其反射系数的大小与频率的关系如下图所示。
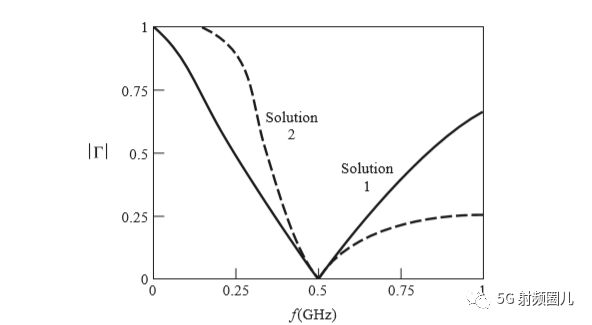
如果单纯从匹配角度来说,两种方案都可以选择,匹配带宽没有明显的区别。 但是实际应用中,可以根据射频电路的需求进行选择。 比如是否需要隔直? 是否需要滤波? 实际电感和电容的选型等等。
No4.3 短截线匹配法
用集总参数元器件进行阻抗匹配,大家理解起来比较容易,但是在微波电路中,我们常常不喜欢加进去那些林林总总的电感电容,一个原因是贵,另一个原因则是对应值的电感电容很难取寻找。我们通常希望直接在线上进行匹配。今天,我们一起来看一下如何利用一段传输线来进行阻抗匹配?
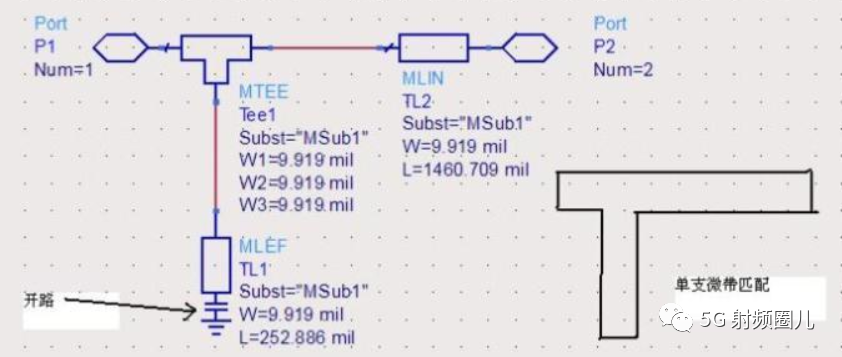
最常用到的短截线匹配法有单支节和双支节,有双支节了,当然还会有多支节。我们就最常用的单支节和双支节进行讨论。
单支节就是使用单个开路或者短路的传输线段在距离负载某一确定位置处,通过与传输线的并联或者串联,实现阻抗匹配。如下图所示。在这种单支节短截线匹配电路中,有两个可调节的参数,第一个是从负载到短截线的距离d,第二个就是短截线所能提供的电纳或者电抗,短截线所能提供的电纳或者电抗实际上是由短截线本身的特性阻抗Z0和短截线的长度决定。因此,单支节短截线匹配法实际上是对短截线到负载距离d和短截线特性阻抗Z0,以及短截线长度L这三个参数组合优化。
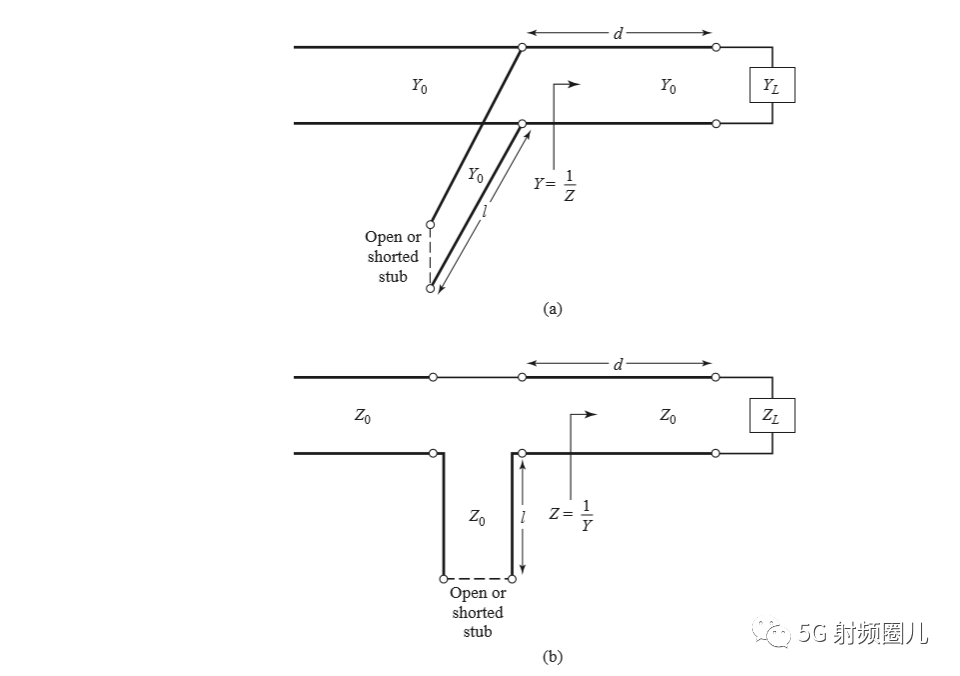
对于并联短截线,其基本思路是首先确定短截线到负载的距离d,在此点向传输线方向看过去的导纳为:Y=Y0+jB,然后选择短截线的电纳为-jB,就可以达到匹配条件。
对于串联短截线,短截线到负载的距离d,在此位置,向传输线方向看过去的阻抗为Z=Z0+jX,那么选择短截线的电抗为-jX,便达到阻抗匹配的条件。
另一个就是双短截线匹配。双短截线匹配,增加了设计参量,提高了设计的灵活度。双短截线匹配电路如下图所示,负载到第一个短截线的距离不再有特殊要求,但是两个短截线直接的距离d是有要求的。
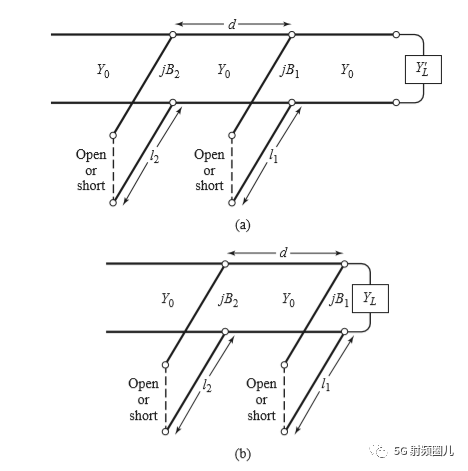
在《微波工程》中,作者通过两个例子,利用Smith圆图对单路短截线的参数进行求解。具体过程,请参照书籍。推荐在设计中,利用仿真软件进行匹配,因此,理论推导过程不再赘述。
No4.4 四分之一波长阻抗变换器
常用的阻抗匹配方法很多,我们今天一起来学习下四分之一阻抗变换器匹配的原理。
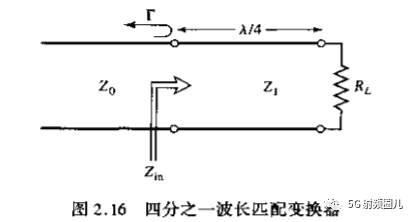
四分之一波长阻抗变换器是有一段长度为lambda0/4,阻抗为Z01的传输线构成,其中Lambda0是传输线所传输信号的中心频率所对应的相波长,与信号频率f0,传输线的结构,填充介质等因素有关。 当传输线的终端接纯电阻负载RL时,在中心频率上的输入阻抗为:
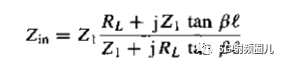
为了计算该式在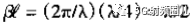 时的值,我们可以用
时的值,我们可以用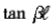 去除上式的分子分母,并取
去除上式的分子分母,并取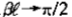 的极限,即可得:
的极限,即可得:
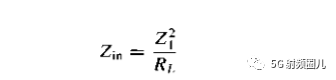
为了使反射系数等于0,必须有Z0=Zin,可得四分之一波长变换器的特性阻抗为:
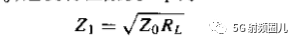
可以看出了,这个阻抗就是负载阻抗和传输线阻抗的几何平均。 因此在传输线上就没有驻波,反射系数为0,但是在四分之一阻抗变换器内还是有驻波存在。 变换器上的驻波系数为:
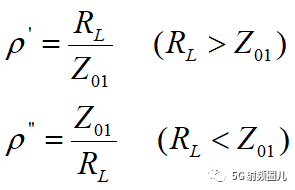
注意:上式是基于信号的中心频率f0来求解的,因此只能在这个点上实现匹配,或者匹配线的长度是该频率的四分之一波长或者四分之一波长的奇数倍(2n+1)处实现完全匹配,在其他频率上将会失配。
上式只能用于实阻抗匹配,即负载的阻抗为纯电阻。 但是对于一般的复阻抗负载,ZL=RL+jXL,时,一般先经过一个适当长度的传输线把负载阻抗变换为实阻抗负载。 下面介绍两种常用的匹配方法:
方法一:终端接四分之一波长阻抗变换器的同时,并联一段特性阻抗为Z0,长度为s的终端段路线。
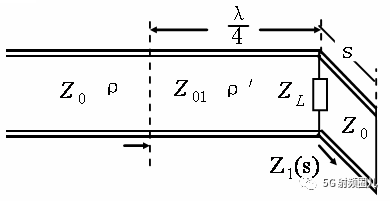
终端短路线在负载处提供一个纯电抗,只要选择合适的长度s,就可以使其在负载处所呈现的电抗来抵消负载的电抗部分,从而使负载的总阻抗为实数,然后利用四分之一波长阻抗变换器将负载处的等效阻抗变换为Z0,实现阻抗匹配。
方法二:在靠近终端的电压波腹点或者波节点处接入四分之一波长阻抗变换器来实现复阻抗匹配。
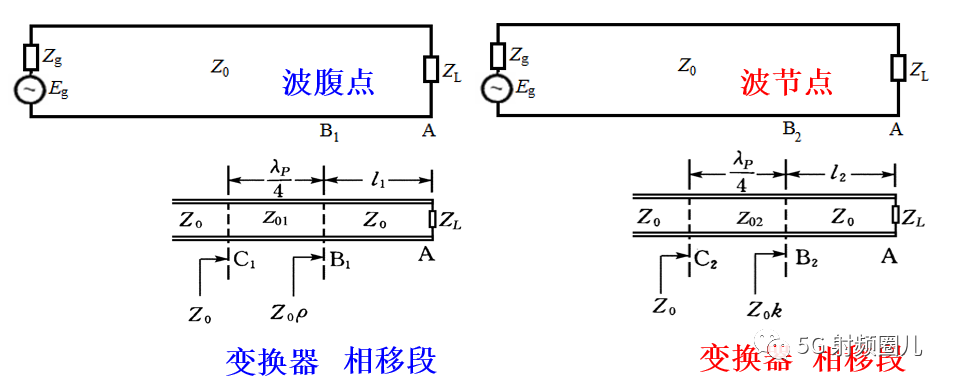
传输线上电压波节点或者波腹点的阻抗为实数,所以如果在这两个位置剪短传输线,接入特性阻抗为Z01的四分之一波长变换器就可以进行阻抗匹配。 负载与电压波节点或者波腹点位置的传输线称为相移段。
1,当电压波腹点接入四分之一波长变换器时,相移段长度L和变换器特性阻抗分别为:
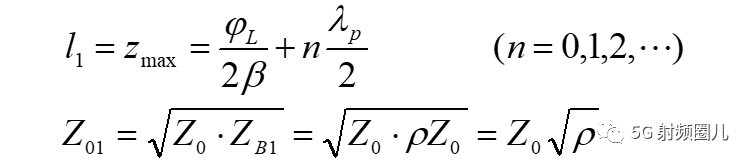
2,当电压波节点接入四分之一波长变换器时,相移段长度L和变换器特性阻抗分别为:
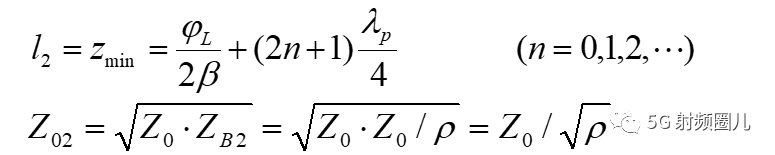
这个时候阻抗变换器上的驻波系数为:

为了更深入的了解四分之一波长阻抗变换器的特性,我们一起来看一下多次反射的概念。
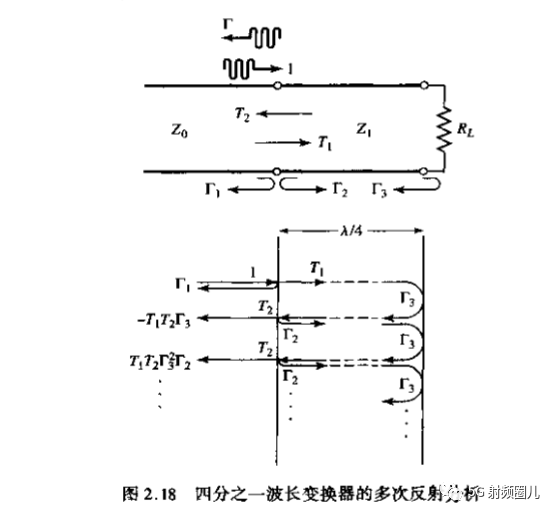
对于上图给出的四分之一波长变换器,它具有一下的反射系数:

这些反射系数可以表示为:
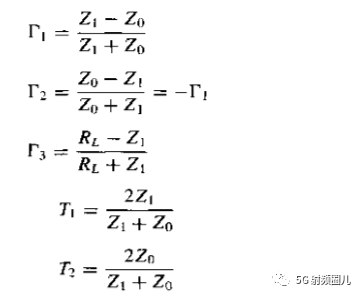
我们可以想象一下,当电磁波信号沿着传输线进入四分之一波长变换器时,它首先看到的阻抗是Z1,因为还没有到达负载RL,因而负载还看不到它的影响。 一部分电磁波被反射,另一部分被传输进入四分之一波长变换器,然后被传输的电磁波到达负载时遇到了组在阻抗RL,再次被反射,经过四分之一波长到达传输线和变换器的交界处,遇到阻抗Z0,再次被反射回到负载,电磁波在变换器内不断额被反射吸收,每次反射波都要经过往返两次四分之一波长,产生相位差180°,总的反射系数就是这无数次反射系数的和:
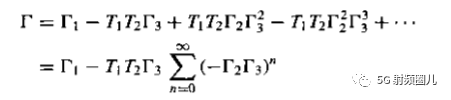
经过一系列的计算:

我们发现,当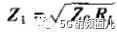 时,上式为0,那么总的反射系数也为0,传输线是匹配的。
时,上式为0,那么总的反射系数也为0,传输线是匹配的。
那么我们发现四分之一波长变换器匹配的原理就是通过选择恰当的匹配段的特性阻抗,和长度,使得所有的部分反射的结果叠加为0,来消除组播,形成整个传输线上的行波。 可见变换器内部的斗争还是蛮激烈的。
小结:其实到这里,阻抗匹配还远远没有结束。 在很多的射频电路中,宽带阻抗匹配才更利于整个系统设计。 但是最为高级的一个阻抗匹配方式就是滤波器的设计。 让我们在以后的章节慢慢完善阻抗匹配吧。
审核编辑:汤梓红
全部0条评论

快来发表一下你的评论吧 !
