

电子说
协方差矩阵
方差衡量一个变量在自身之间的变化,而协方差衡量两个变量(a和b)之间的变化。
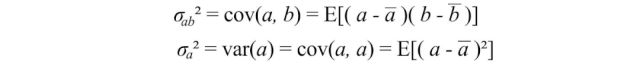
我们可以将所有可能的协方差组合保存在一个称为协方差矩阵Σ的矩阵中。
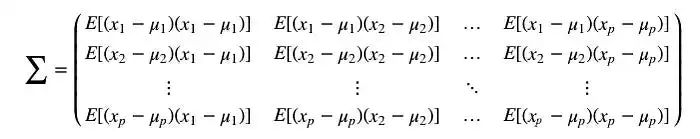
我们可以将这个简单的矩阵形式重写为:
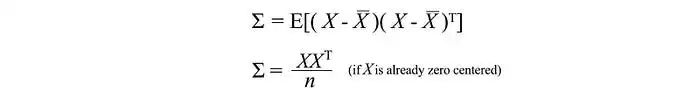
对角线元素保存单个变量(如身高)的方差,而非对角线元素保存两个变量之间的协方差。现在让我们计算样本协方差。
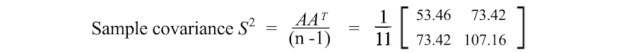

正的样本协方差表明身高和体重是正相关的。如果它们是负相关的,协方差将为负数;如果它们是独立的,则协方差为零。
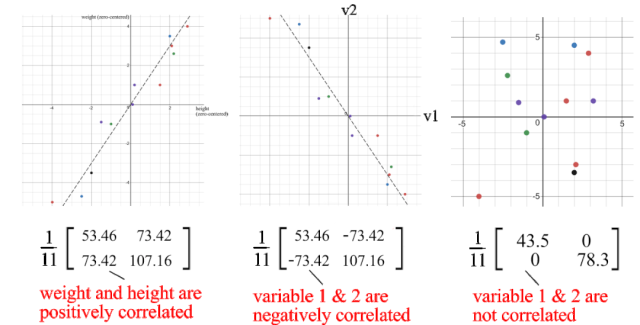
协方差矩阵和SVD
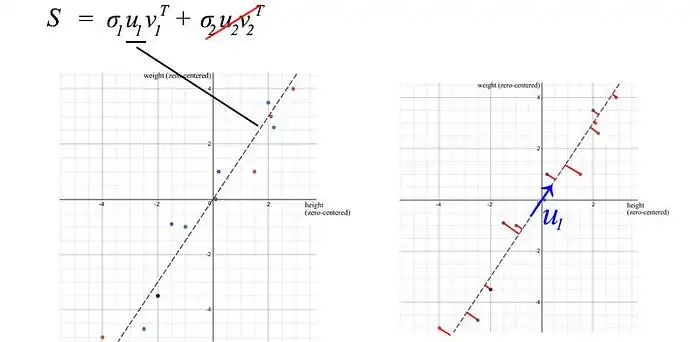
我们可以使用SVD来分解样本协方差矩阵。由于σ₂相对于σ₁而言相对较小,我们甚至可以忽略σ₂项。当我们训练一个机器学习模型时,我们可以对身高和体重进行线性回归,形成一个新属性,而不是将它们视为两个分离且相关的属性(纠缠的数据通常使模型训练更加困难)。
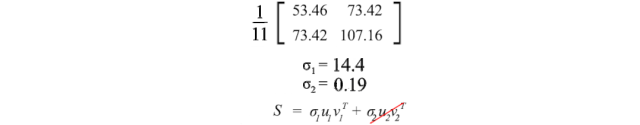
u₁有一个重要的意义,它是S的主要成分。

在SVD的背景下,样本协方差矩阵具有一些特性:
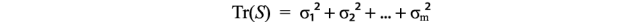
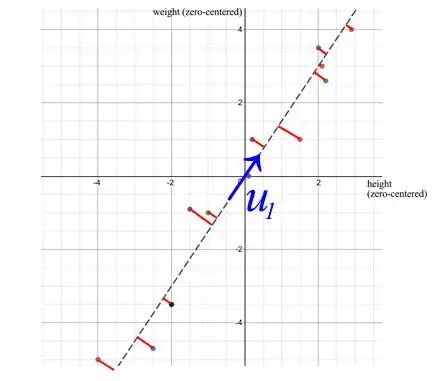
性质
协方差矩阵不仅对称,而且还是正半定的。因为方差是正数或者零,所以uᵀVu始终大于或等于零。通过能量测试,V是正半定的。
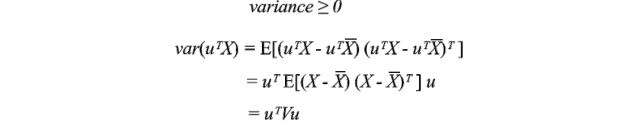
因此,
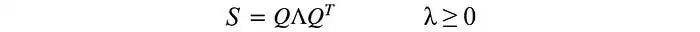
通常,在进行某些线性变换A之后,我们想知道转换后数据的协方差。这可以用变换矩阵A和原始数据的协方差来计算。
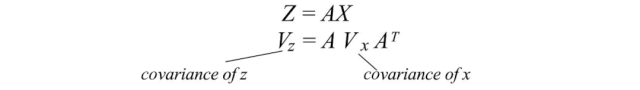
相关矩阵
相关矩阵是协方差矩阵的标准化版本。相关矩阵对变量进行标准化(缩放),使它们的标准差为1。
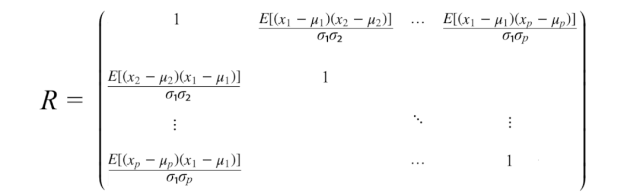
如果变量的量级相差很大,那么将使用相关矩阵。糟糕的缩放可能会损害梯度下降等机器学习算法的效果。
可视化
到目前为止,我们有很多方程式。让我们将SVD的作用可视化,并逐渐开发我们的洞察力。SVD将矩阵A分解为USVᵀ。将向量x(Ax)应用于A可以被视为对x执行旋转(Vᵀ),缩放(S)和另一个旋转(U)。
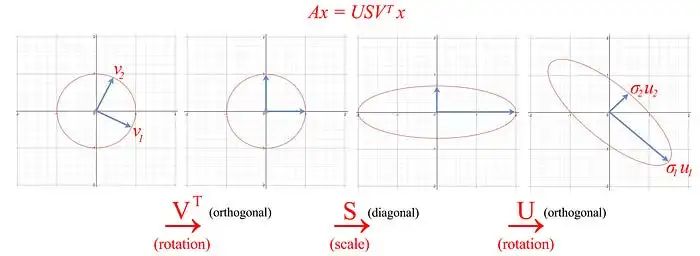
如上所示,矩阵 V 的特征向量 vᵢ 被转换为:
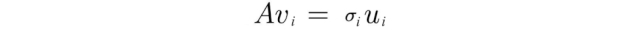
或者以完整矩阵形式表示
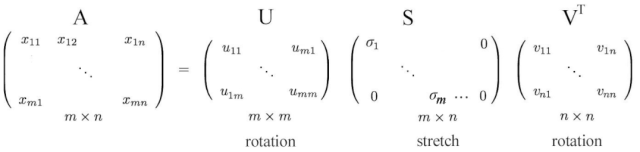
r = m < n
奇异值分解(SVD)的洞察
如前所述,SVD 可以表示为
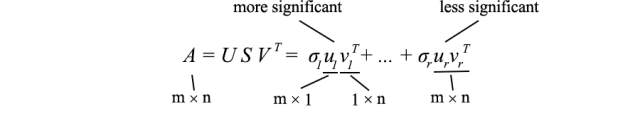
由于 uᵢ 和 vᵢ 的长度为单位长度,确定每个项的重要性的最主要因素是奇异值 σᵢ。我们故意按降序对 σᵢ 进行排序。如果特征值变得太小,我们可以忽略剩下的项(+ σᵢuᵢvᵢᵀ + …)。
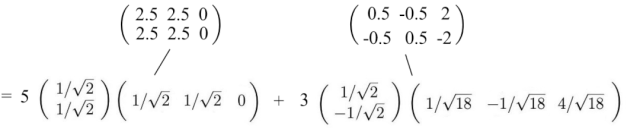
这种表示法具有一些有趣的含义。例如,我们有一个矩阵,其中包含不同投资者交易的股票收益率。

作为基金经理,我们可以从中获取什么信息?寻找模式和结构将是第一步。也许,我们可以找到具有最大收益的股票和投资者的组合。SVD 将 n × n 矩阵分解为具有奇异值 σᵢ 表示其显著性的 r 组件。将其视为一种将纠缠和相关属性提取到更少的无关联的主要方向的方法。
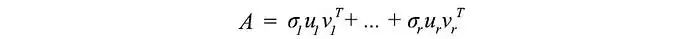
如果数据高度相关,我们应该期望许多 σᵢ 值较小且可以忽略。
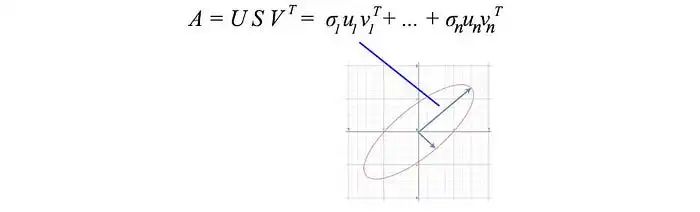
在我们之前的例子中,体重和身高高度相关。如果我们有一个包含 1000 人体重和身高的矩阵,SVD 分解中的第一个组件将占主导地位。如我们之前讨论的那样,u₁ 向量确实表示了这 1000 人之间体重和身高的比例。
主成分分析(PCA)
从技术上讲,SVD 分别提取具有最高方差的方向中的数据。PCA 是将 m 维输入特征映射到 k 维潜在因子(k 个主成分)的线性模型。如果我们忽略不太重要的项,我们将去除我们不太关心的组件,但保留具有最高方差(最大信息)的主要方向。
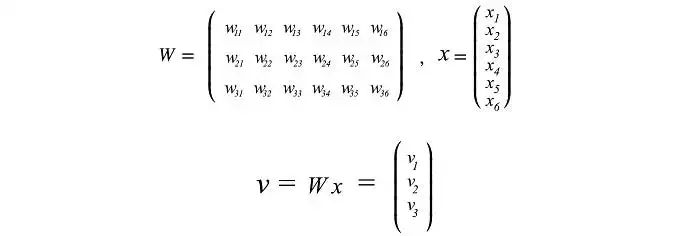
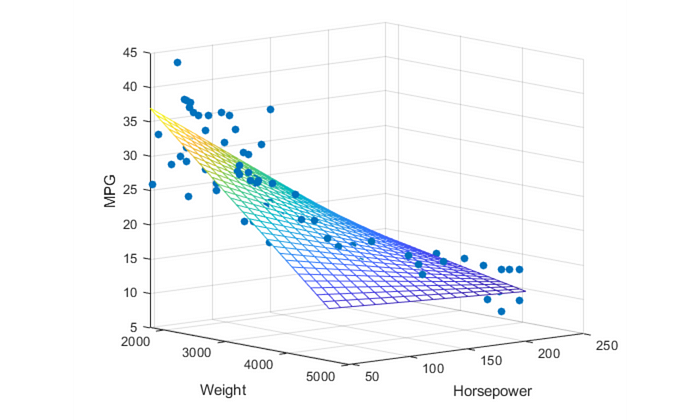
考虑下面显示为蓝色点的三维数据点。它可以很容易地用一个平面来近似。
您可能很快就会意识到,我们可以使用 SVD 找到矩阵 W。考虑下面位于二维空间的数据点。
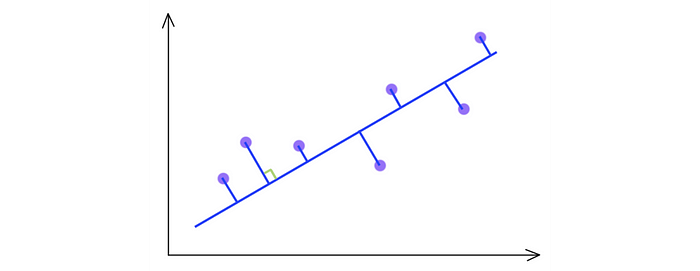
SVD 选择最大化输出方差的投影。因此,如果 PCA 具有更高的方差,它会选择蓝线而不是绿线。
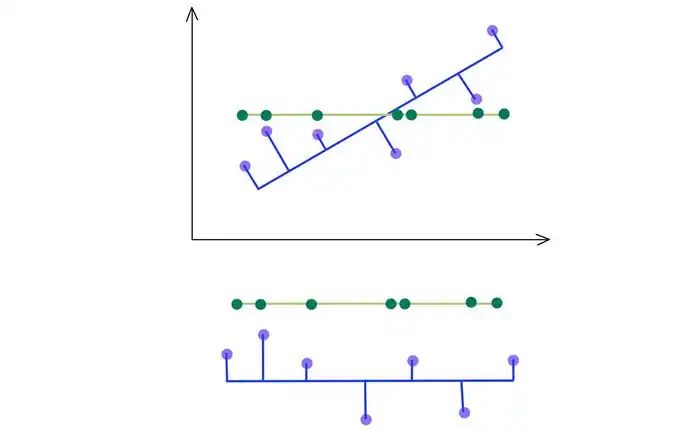
如下所示,我们保留具有前 kth 最高奇异值的特征向量。
利率
让我们通过回顾一个关于利率数据的例子来更深入地说明这个概念,该数据源自美国财政部。从 3 个月、6 个月、…到 20 年的 9 种不同利率(基点)在连续 6 个工作日内进行了收集,其中 A 存储了与前一天相比的差异。A 的元素在此期间已经减去了其平均值。即它是零中心的(沿着其行)。
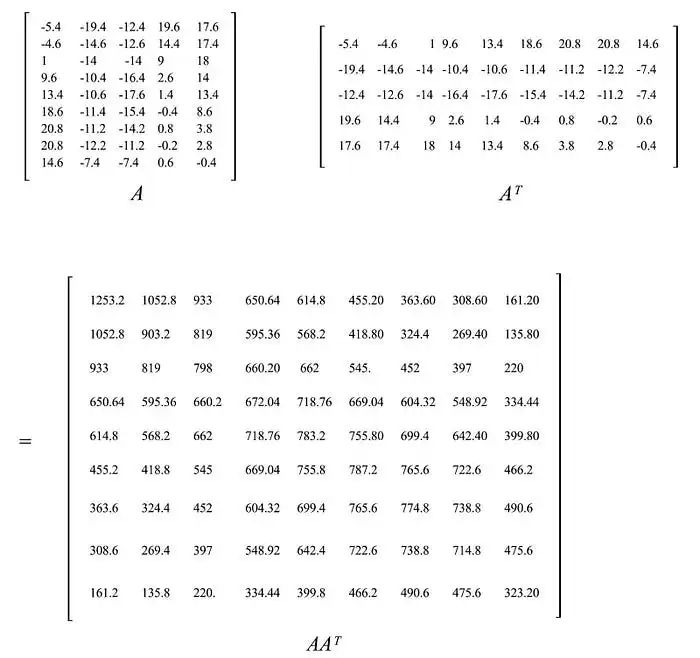
样本协方差矩阵等于 S = AAᵀ/(5-1)。

现在我们有了想要分解的协方差矩阵 S。SVD 分解为

从 SVD 分解中,我们意识到我们可以关注前三个主成分。
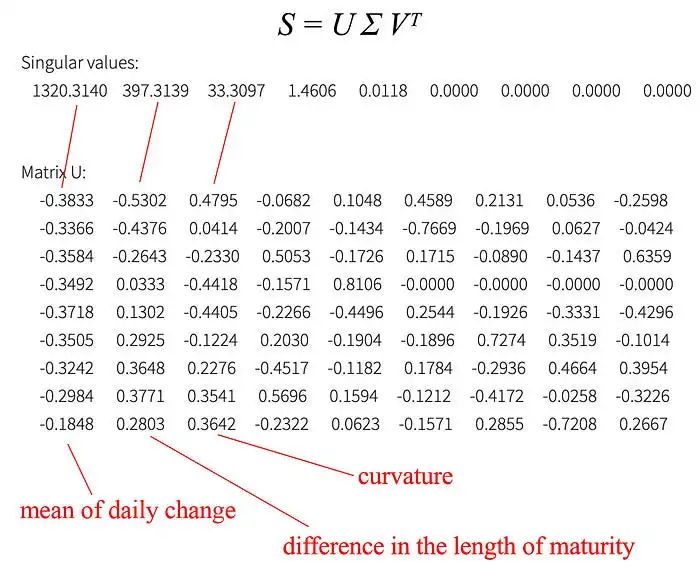
如图所示,第一个主成分与所有到期长度的日常变化的加权平均值有关。第二个主成分调整了与债券到期长度敏感的日常变化。(第三个主成分可能是曲率 - 二阶导数。)
我们在日常生活中很了解利率变化和期限之间的关系。因此,主成分重新确认了我们相信利率如何运作。但是当我们面对陌生的原始数据时,PCA 对于提取数据的主成分以找到底层信息结构非常有帮助。这可能回答了如何在大海捞针的一些问题。
提示
在执行 SVD 之前,对特征进行缩放。
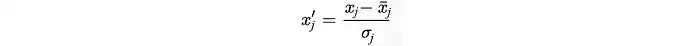
假设我们想保留 99% 的方差,我们可以选择 k,使得
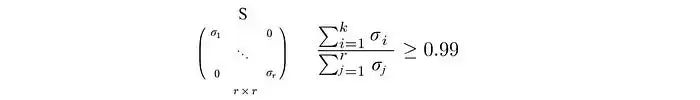
全部0条评论

快来发表一下你的评论吧 !
