

下图是我们常见的用于仿真OP的AC特性(DC增益、GBW等)的Bench。我们通过在OP的输出和输入之间串联一个一阶RC网络(R、C值通常都很大)的形式组成一个闭环系统,而我们需要的其实是OP的开环特性。
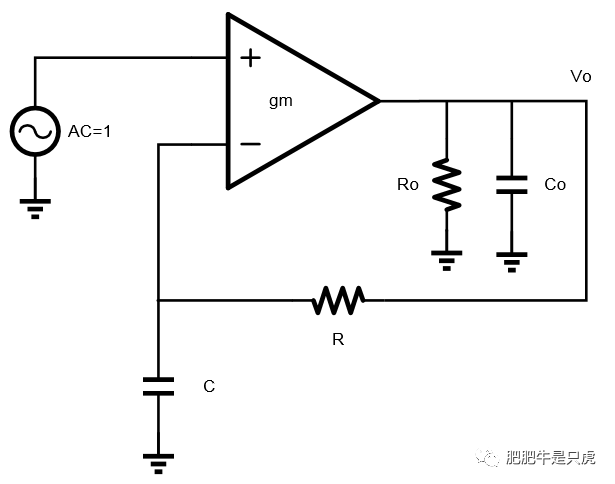
本文试图弄明白以下几个问题:
为何通过闭环的方式可以得到OP的开环AC特性?
R、C对仿真结果有什么影响?
R、C要取大,那到底要多大?这个问题和上面的问题关联度很大。
问题很基础,过程很重要,答案不简单。
先推导这个Bench的闭环传函:
这是一个电压-电压负反馈,其闭环系统的传函可以用标准反馈方程Y/X=G/(1+G*β)来统一。
第一步:先断环,考虑加载效应,见下图
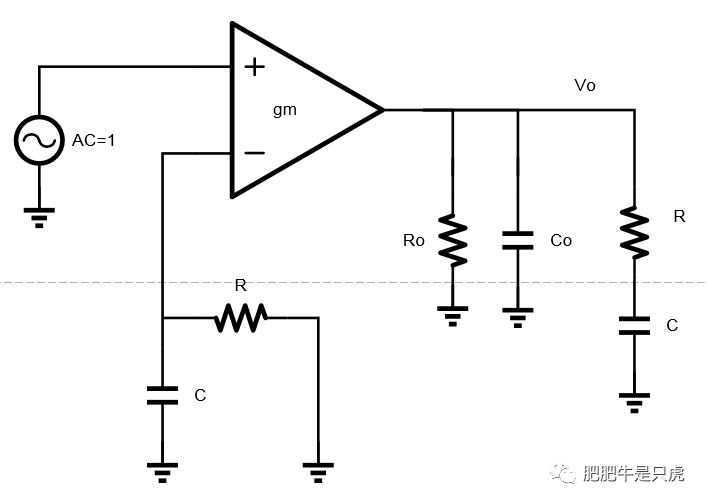
第二步:计算前馈增益G(s),对于VV反馈,其实就是OP的开环增益,如下:
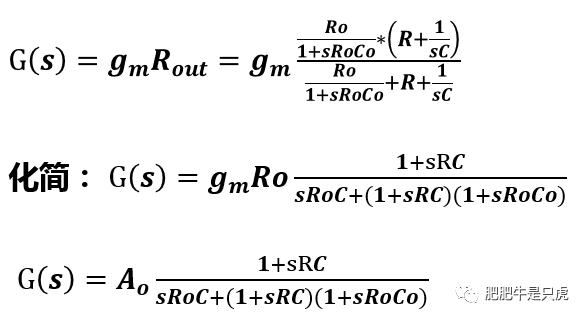
第三步:计算反馈系数β(s)
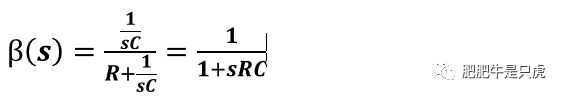
第四步:计算闭环增益A(s),A(s)=G(s)/(1+G(s)*β(s))

至此,我们得到整个系统的闭环传函,上面的推导过程中仅仅做了如下近似:
RC>>RoC,且RC>>RoCo,
由于R和C都是很大的值,这个近似误差可以忽略不计。
接下来,该分析闭环传函了
我们尝试盯着闭环传函A(s)的表达式看,能看出点啥?
闭环传函有一个LHP零点:z=-1/RC
闭环传函分母是一个标准的二阶形式,有2个根,对应着2个LHP极点,
假设分母的两个极点分别为p1和p2,且|p1|<<|p2|,则
p1+p2=-1/(Ro*Co)≈p2
p1 p2=Ao/(Ro R C Co)
联合上面两个式子,不难得到:
p1=-Ao/(R*C)
p2=-1/(Ro*Co)
至此,我们得到了整个闭环系统的零极点分布情况,总结下:
z=-1/(RC)
p1=-Ao/(R*C)
p2=-1/(Ro*Co)
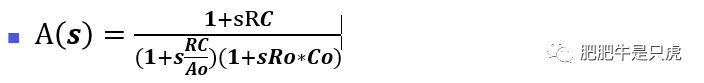
不难看出,p2是OP本身的输出极点,z和p1的频率极低,构成一对低频零极点对。当频率远>这一对零极点对之后,A(S)可以简化为:

继续盯着这个表达式看,这个表达式什么意思?
这不就是我们想要的OP的开环AC特性吗?
我们费尽千辛万苦,终于在这一步得到我们想要的。
画个图,可以看得更直观:
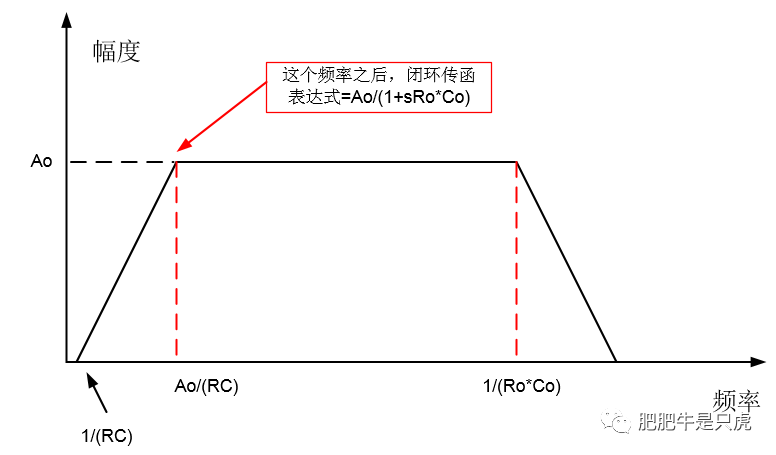
行文到此,问题基本上说清楚了,我们回到文章开头的几个问题,这时候应该有答案了吧!
对于RC的取值问题,我们要保证Ao/(RC)<<1/(Ro*Co)即可。
举个例子:
R1=10^12,
C=1,
OP增益Ao=1000倍(60dB),
则RC造成的低频极点为1000/(10^12)=10^(-9),是一个极低频率的值,低到我们可能压根儿都没发现它的存在。因为我们在跑AC的时候会给定一段频率,比如从1Hz~1GHz,也就是说低于1Hz的波形我们压根儿就没看,所以我们跑完AC观看波形的时候会发现AC曲线低频是平的,并没有我们文章所讲的一对低频零极点。看官如果想看到这一对零极点,从很低频的部分开始跑AC即可,或者把RC的取值取小一点儿。
直观解释
终于到了群众喜闻乐见的“直观解释”环节了,先把Bench拷贝过来,对照着说。

OP正输入端AC=1
OP负输入端AC≈0,为什么呢?因为C很大,阻抗1/(sC)很小,频率稍微高一点,就近似于短路
R的作用:通直流隔交流,R可以将OP的输出和负输入短路,建立直流工作点。但是对于AC而言,大R基本不构成加载效应,不会影响OP增益。
OP正负输入AC=1,所以直接观察OP输出Vo就可以得到OP的增益的开环AC特性。
全部0条评论

快来发表一下你的评论吧 !
