

本应用笔记讨论热敏电阻在温度补偿中的应用,简要介绍快速确定最佳电路条件的遗传算法。通过一个实例可以看出,利用该算法可以很容易得到最佳电阻值和NTC热敏电阻值,实现特定的电压温度关系曲线。
简介
问题:对于图1所示电路拓扑,如何获得电阻值和NTC热敏电阻值,以实现图2所示的电压与温度关系曲线(注意:或许只能使用标称值)?
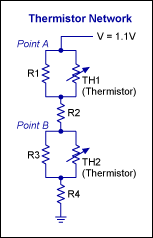
图1. 热敏电阻网络
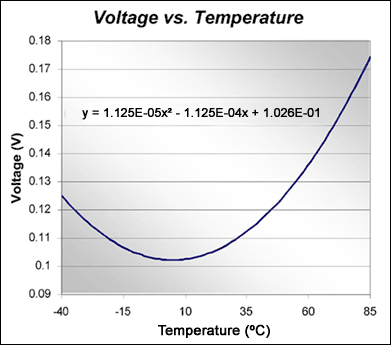
图2. 电压与温度关系曲线
这个问题也许不会出现在教科书中,但是当采用热敏电阻网络对有源元件进行温度补偿时,就会面临这样一个实际问题。有人可能会按照图1电路,通过不断的电路实验和无数个方程的求解来确定方案;有些人可能会将数值代入仿真器或电子表格,然后通过慢长的调整后得到尽可能匹配的曲线。
考虑到上述方案涉及到的众多变量和温度效应,利用上述任何一种方法寻求这个电路的最佳方案都将充满挑战。实际设计中只能采用标称值,也在一定程度上增加了难度。针对某组条件求解电路方案也许是一种可以接受的途径,但当条件、网络或预期响应条件较多时,求解过程就变得单调乏味。网络越复杂(为了得到更好的温度响应),求解最佳方案的过程也更困难或更耗时,甚至无法得到象征性或经验性的数据。而利用数值方法,例如:遗传算法,可以方便地解决这些问题。
遗传和电路这两个词很少会用在同一场景,但是,如同下文将要看到的,遗传算法可以用来求解图1所示电路的元件值。本应用笔记将讨论温度补偿时热敏电阻的使用,并简要介绍遗传算法,最后会通过算法的一个实例快速求解上述问题。
热敏电阻网络的应用
需要进行温度补偿的系统大多选用热敏电阻网络。比如,热敏电阻网络可以用来调整电源电压、PWM输出等,也可以为晶体管、放大器、激光二极管等提供经过温度补偿的偏置电流。热敏电阻网络具有如广泛的应用,而每个应用、每个设备所需要的补偿(网络值)却不尽相同。
图2所示范例是光通信链路中激光二极管的补偿电路。为了保证通信质量,激光二极管的偏置电路必须随着温度的变化进行调整。温度补偿后的偏置电流可以采用图3所示电路注入激光器,但是,为了使目标电压与温度一致(图2),必须确定最佳数值。通过遗传算法可以在几秒钟内找到近乎理想的方案。
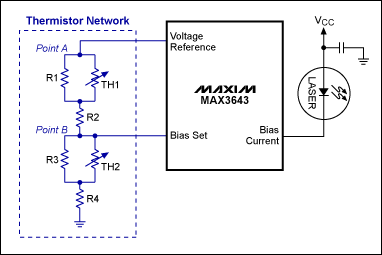
图3. 采用MAX3643突发模式激光驱动器的热敏电阻网络
遗传学算法
遗传算法是一种最优化算法,它通过模拟遗传过程找到解决多变量问题的最佳方案。虽然遗传算法早在1950年, ¹ 就被首次使用,但也只是在最近的15到20年,由于计算机技术和处理器速度的发展,才得到广泛应用。
按照最简单形式,算法首先创建一个随机的群体或一个有预定起始点的群体。群体(图4)中的每个群体单元(个体)由一列可以确定其结构(其遗传代码)的变量组成。一旦群体单元完成初始化,就可以通过一系列标准衡量它的特性,并与其它单元进行比较。群体单元随后根据它们的特性进行分类,排名差的个体将被去除(自然淘汰),同时通过混合来自前一代中最佳群体单元的变量(基因代码)会生成新一代的个体(图5)。
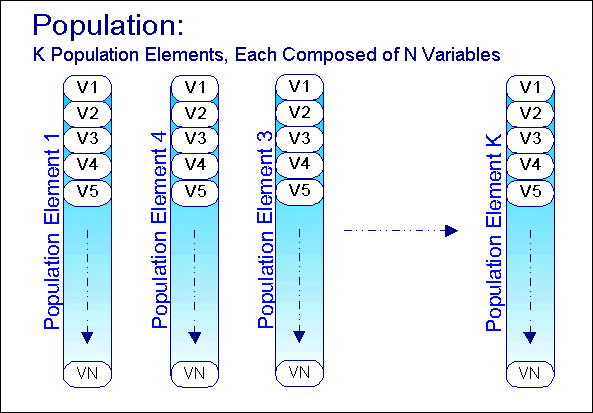
图4. 具有K个群体单元,每个单元由N个变量组成的群体示例
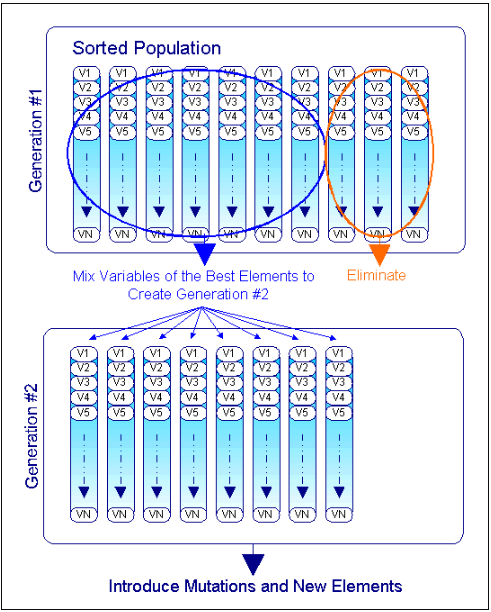
图5. 从上一代到下一代变量(比如遗传代码)混合的过程示例
如果过程在完成各步骤后容许循环,那么群体将会很快在一个共同且唯一的遗传代码上饱和。由此可以得到一个最小值,但它或许不是总体最小值。为了防止群体饱和或收敛于一个局部的最小值,必须在群体中引入新的随机单元和对群体单元变量的突变(图6)。
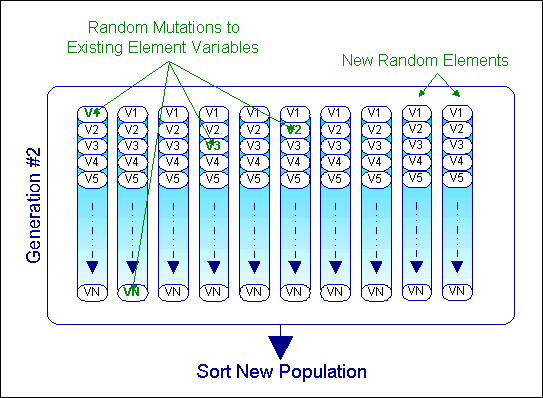
图6. 在一代群体中引入随机单元的过程示例
每个应用中应该引入的随机因素在频率和数量上都不同。如果引入的随机因素过多,那么算法将无法收敛于一个理想的方案;如果引入的太少,找到总体最小值将会需要很长时间。因此,引入的随机量应该通过反复试验调整,或者当群体饱和度增加时动态引入更多的随机性。
还有一些优化算法比遗传学算法速度更快,但是,它们通常对于多变量问题来讲编程更加复杂,并且通常收敛于一个局部最小值。遗传学算法克服了这些问题。
遗传学算法基于一个随机过程,所以收敛于一个绝对最佳方案所需的时间也是随机的。平均收敛时间将会随着每一个群体单元的变量数目的增加而增加。对于某些应用来讲,针对某个特定情况确定、计算特性标准也很困难。简而言之,有时很难用方程式表示出最佳方案。对于简单的有源电路,比如图1所示的热敏电阻电路,可以很好地定义并很容易写出特征标准。考虑到变量数量,在一个合理的时间段内就可以找到解决方案。因此,遗传学算法很适合解决这种类型的电路。
实例
利用免费的visual basic编译器,² 可以通过一段例程求解热敏电阻网络值(图1),使其与图2所需的响应匹配。本例的源程序和可执行文件可供下载。
软件采用的算法基于下面的基本步骤:
将可用的电阻值和热敏电阻值定义为每个群体单元的可能变量,为可用的电阻和可用的热敏电阻分别定义一个数组。
建立个体的一个随机群体(对于本例,群体应该包含有100个单元)。每个群体单元就是一个数组,其中包含电路中(图1)每个元件的入口。
使不同温度下网络所需的电压值或电阻值与之相等,画出响应特性;然后将所需的电压值/电阻值代入多项式方程代码中。
计算每个群体单元的均方根误差
从最低误差到最高误差将群体排序,用图形表示最佳方案。
去除最差方案,然后随机或系统地将剩余单元组合,生成下一代群体单元。
通过引入新的随机群体单元或者通过随机改变一个或者多个现有群体单元的一个或多个变量来引入随机性。
返回步骤4并重复,直至均方根差足够低,用户决定停止这一过程。
到了这一步您也许会提出疑问:"如何解决网络值问题?"。如同遗传和进化一样,这个方案是从一个状态"成长"到另一个状态。最佳方案本质上就是针对环境(所需的电流响应)的最佳遗传代码(电路元件值)。如果仍然感到困惑,那么好吧,通过下面的实例结果很快就会消除您的担忧。
图7所示为软件的图形用户界面。通过这个界面,可以选取热敏电阻网络的配置,并通过一个多项式输入预期的响应。可以通过选择求解所有的电阻或某个电压,需要优化的温度范围以及是否选用1%或5%倍增电阻值。点击"Run"按钮开始算运行算法。随着程序的运行,均方根误差、迭代次数以及当前最佳方案的元件值都会不断更新。
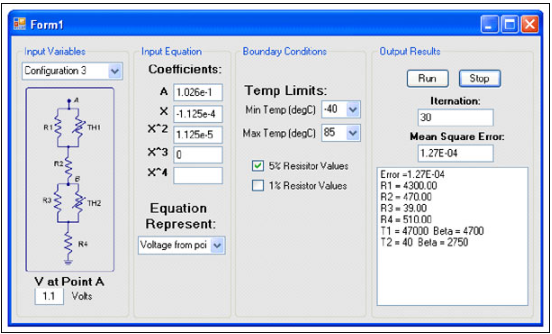
图7. 应用软件简化了求解热敏电阻值与所需响应匹配的过程
同时还会生成预期的响应曲线(绿色)和当前最佳的方案曲线(红色)。图8所示为计算机运行30次迭代后的图形输出。从图中可以看到,响应并不理想。图9为经过500次迭代后得到的一个非常好的响应,大概需要10秒钟。可以需要稍微暂停一下,然后继续运行程序,图10所示为运行结果,它已经近乎完全匹配。
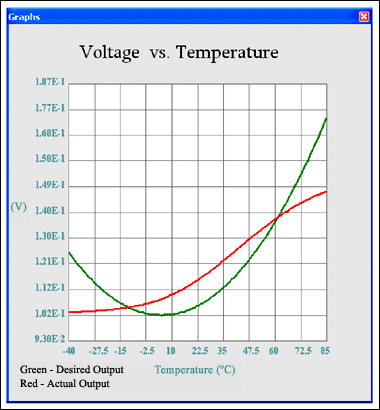
图8. 经过30次迭代后实际与预期的电压温度关系曲线
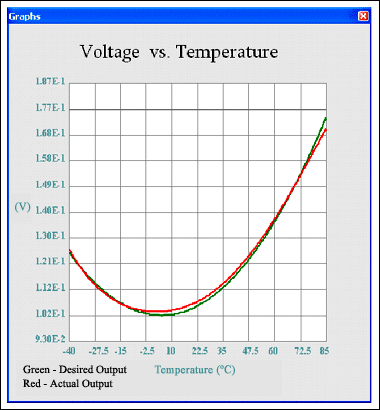
图9. 经过500次迭代后实际与预期的电压温度关系曲线
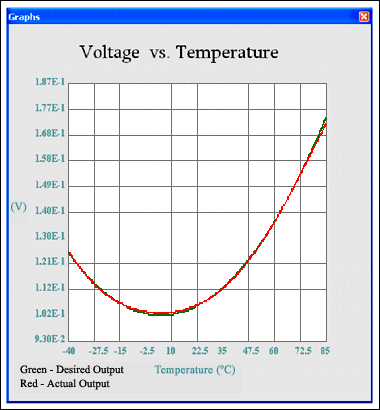
图10. 实际与预期的电压温度关系曲线非常匹配
以图1为例,方案中包含下列元件值:
R1 = 8.2k, R2 = 3.6k, R3 = 2.2k, R4 = 1.1k
TH1 = 47k Beta = 4700, TH2 = 40 Beta = 2750
不同测试,收敛速度也不一样。对于较简单的网络收敛速度较快,对于稍复杂的网络,或者使用了1%电阻值,因为有更多的变量可供选择,所以通常需要的收敛时间较长。
考虑到上述所有因素,由两个热敏电阻和四个电阻组成的网络,在只使用标称值情况下,可以在不到30秒的时间内近似匹配预期的温度响应。
如果您仍然对遗传学算法解决电路问题感到疑惑,请下载程序,亲自尝试一下。您可能会对遗传学算法在热敏电阻网络方案中的快速求解过程感到惊讶。
审核编辑:郭婷
全部0条评论

快来发表一下你的评论吧 !
