FIR滤波器在信号处理和通信系统中的应用

FIR滤波器在信号处理和通信系统中有着极为广泛的应用，全称是有限长单位冲击响应滤波器。

FIR滤波器的缺点是运算量大，但结合目前的芯片技术，FPGA自然不必说，可以非常灵活的设计很高阶次的并行结构，ASIC和GPU都是高密度的流水线型DSP处理，对于FIR所要求的高运算能力，自然是不在话下。另一个缺点在于对于低频信号处理显得有一些力不从心。

FIR滤波器的优点在于阶次可以做的很高，并且很容易得到各种各样期望是的响应曲线，很灵活，并且通过调整窗函数，可以得到很好的滤波效果。

FIR滤波器可以说是和卷积相当紧密的联系在一起的，可以说FIR是完全依托于卷积的概念而生的一种滤波器。并且由于傅里叶前辈的贡献，我们可以很简单的用FFT来计算大长度的FIR，也因此在通信系统的信号处理中随处可见FIR的身影。

滤波

想要把一个知识点发散出去，那就得对它认识的足够深刻。作为一个硬件工程师，对于滤波的概念再熟悉不过了，所谓滤波，就是滤掉不想要的杂波，留下我们想要的信号。

但是如果我不能给别人讲出一点更深层次的东西，也辜负了别人关注我一番。从频域上来讲，信号是一个矢量，滤波的目的在于只保留这个矢量的某些分量，而滤掉其他分量，得到其在子空间内的投影。

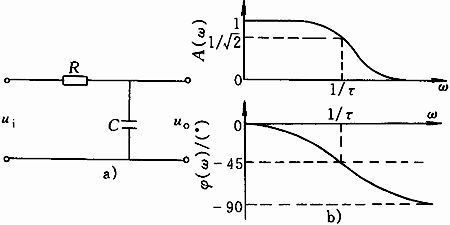
举个简单的例子，一阶低通滤波。一阶低通滤波是怎么实现的？在对输入信号做了延时之后再叠加回去，就得到了滤波之后的结果。信号在时间上的延时就相当于相位上的滞后，参照上图的频率响应曲线。当相位的滞后到了180°时，和原本的信号做叠加，得到的结果就是0，于是就被滤掉了。

把一阶低通滤波抽象到离散系统中，采用数字的方式来实现，其数学表达式是Y(n)=a*X(n)+(1-a)*Y(n-1)。这个结果在我大三的计算机控制课上有过详细的推导过程，但我没记住，自己推了半天也没推出来，索性就直接放个结果吧。可以看到，一阶低通滤波的本质是把输入信号和上一次的输出信号做一个加权，通过调不同的加权系数来调整滤波器的带宽。

数字滤波器可以认为是直接用数学语言来对信号进行滤波，所以其使用和实现上与电路搭建的滤波器有着本质的差别。例如上面的一阶低通滤波，用程序实现的话可以实现任意的带宽设计，而用RC电路实现就会严重受限于器件的工艺。所以把滤波器引申到数字处理之后可以得到这样的定义：滤波器的本质是对频率的加权叠加；和期望的响应曲线做相关。这两句话想不通也没有关系，下面还会继续介绍。

卷积

卷积对于工程学来讲可以说是大厦的根基一般，往广义了来讲，可以说世界上一切都是卷积的结果。

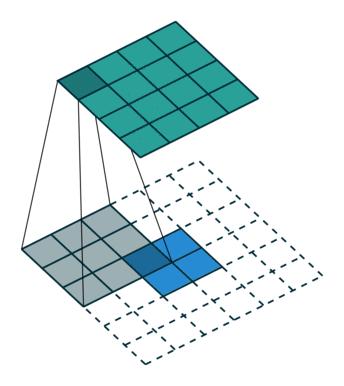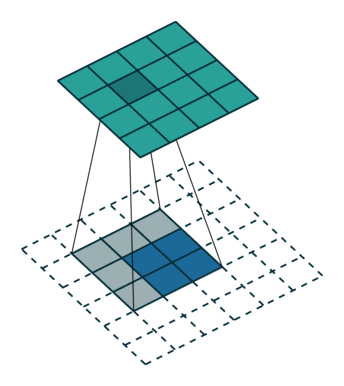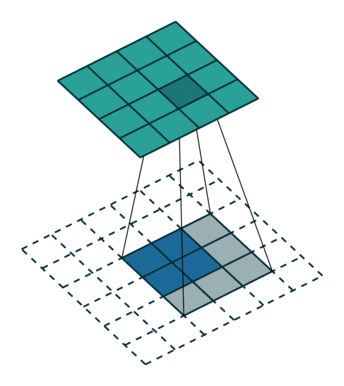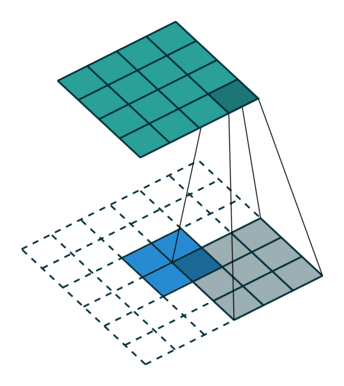
上图是卷积运算的一个示意图。那么卷积的物理意义是什么？我看到过很多很多的解释，但回头来看，这些解释，懂得人看起来觉得说的没问题，不懂的人还是看不懂。我这里举一个例子来说明什么是卷积：小哪吒很皮，这天偷跑出去，在城里惹了祸，把别人家房子弄塌了，李靖给人赔礼道歉修房子，回到家打了小哪吒一顿，屁股肿了，过了两天肿消下去了，没多久又出去惹了祸，抽了敖丙的龙筋，老龙王找上门来，李靖气的又打了他一顿，屁股又肿了，过了半小时，李靖气没消，又打了一顿，老龙王不依不饶，李靖没办法又打了一顿，屁股就肿的越来越高。

在这个例子里，小哪吒屁股肿的程度是最终的输出结果，这个结果不是由李靖的某一巴掌所单独决定的，而是这一天加起来挨的打所共同影响的结果。从最终的结果来讲，第一巴掌的贡献是最小的，最后一巴掌的贡献是最大的。这就是加权叠加。而一巴掌的结果，随着时间的推移，影响会逐渐消散，这是一个一阶惯性环节的响应。整个过程可以抽象为李靖打在哪吒屁股上的巴掌在经过一阶惯性环节之后，不同的输入叠加，最终输出的结果是哪吒现在屁股肿的程度。仅仅一巴掌，大概半小时就消下去了，但是由于李靖打的时间间隔缩小，当无穷小时就是连续的积分，最终的结果是得好几天才能消肿。

所以通俗地讲：卷积就是在输入信号的每一个位置（每一巴掌）处叠加一个单位响应（半小时消肿），把每个位置得到的结果叠加就得到了输出。对于离散系统来讲，卷积的定义是

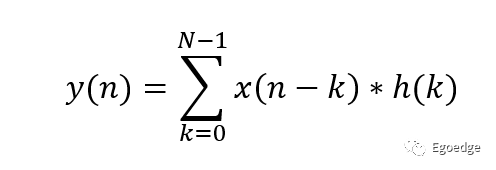
x(n-k)是依次的n个输入，h(k)是每个输入所对应的权值。在滤波的应用中，最简单的就是移动平均数的方式，对相邻的几个历史值做平均加权。这一节最开始放的示意图是图像处理中常用的一种移动平均的滤波方式。

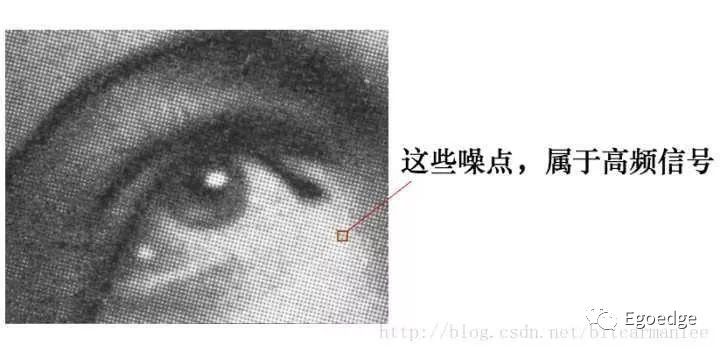
见上图，图中有很多噪点，这些噪点很尖锐，属于高频噪声，将图像提取出来，做成矩阵之后，就可以采用卷积的概念，把每一个点的输出和周围8个点做平均，于是得到如下的结果

FIR滤波器

在理解了卷积的概念之后，FIR滤波器就变得顺理成章。把系统响应的函数换成我们所期望的函数，这样卷积的过程就变成了FIR滤波器。我看到很多地方对滤波的定义是：用一个期望的频率特征函数H(f)去乘以输入信号频率X(f)。对于这个解释我理解了好久，为什么要用一个期望的函数去强行改变输入频率？但现在理解了之后，对这个解释稍作修改之后应该会变得容易理解很多：用一个期望的频率响应去乘以输入信号，这就是滤波。

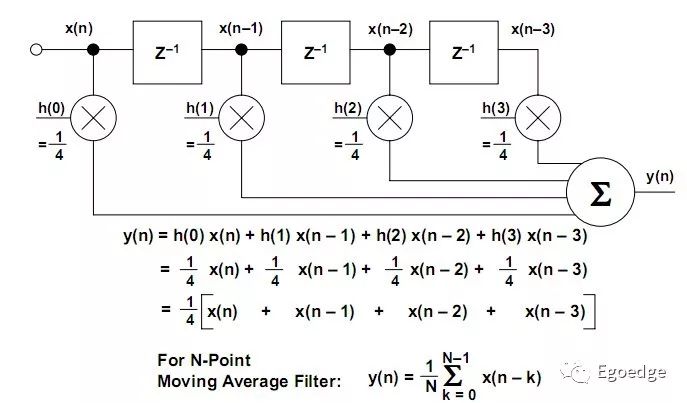
上图是FIR的一个典型的结构，是一个简单的四阶移动平均的FIR滤波器。每次的输出都是对4次历史值的平均。下图分别是经过11阶平均和51阶平均的效果。

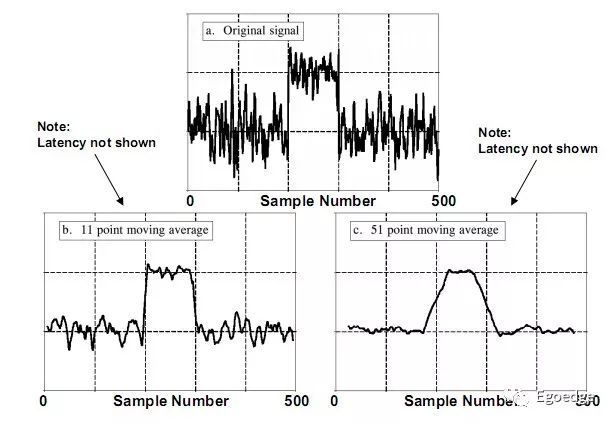
当我们把平均值的响应函数换成我们所期望的响应函数，这样就变成了我们想要的滤波器。我们设计滤波器的过程就是选择FIR中各阶输入的权重值的过程。

FIR滤波器和FFT

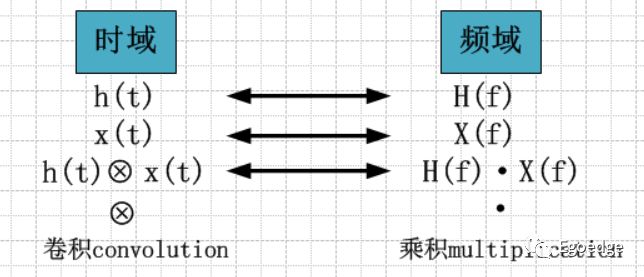
滤波就是用一个期望的频率响应去乘以输入信号的频率，这个定义更明确一点来说是在频域上对滤波概念的解释，而在时域的解释就是用我们所期望的响应函数h(f)做iFFT之后的时域函数H(t)和输入信号X(t)做卷积。可以看到FIR滤波器其实是遵循的滤波在时域上的定义。

傅里叶前辈不仅给我们指出，所有的信号都可以被分解为若干正弦波的叠加，同时还给出了我们时域频域相互变换的方法，其中有一条相当重要的结论就是：时域上的卷积等价于频域上的乘积。因此对于FIR滤波器来讲，我们只需要把输入信号变换到频域，再乘以我们期望的响应函数，再逆变换到时域，就得到了滤波后的结果。

FIR滤波器的设计

在有了FFT的工具之后，我们就可以很方便的进行FIR滤波器的设计。根据上面的说法，我们只需要给定所期望的特征函数h(f)，就可以得到结果，再逆变换回时域，算出不同tap的权值，就得到了时域上FIR的滤波器参数。

FIR滤波器的设计一般有窗函数法、频率取样法和优选法。窗函数法由于其简单直观，应用最多最广泛。举例说明窗函数法的设计应用。

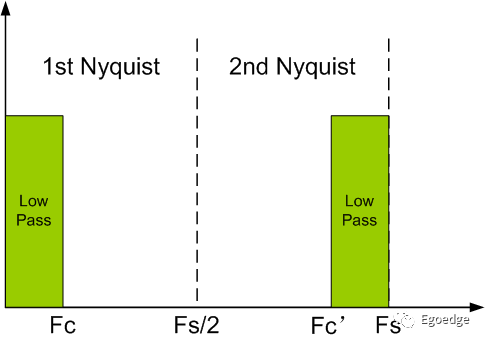
假设我们要设计一个低通滤波器，在频谱上的表示如上图，Fs是采样率，在第一奈奎斯特区内是低通的特性。所谓窗函数法就是加一个滤波器的窗口，如上图所示，对于低通的特性，理想效果是一个矩形窗，低于截止频率通，高于截止频率不通。

假设我们所要设计的滤波器为128阶，截止频率是Fc，在频谱上的表示就是Nc=Fc*(Fs/128)，然后得到期望的特征函数

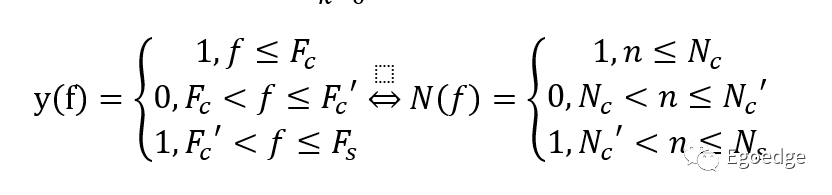
在频域上，用这个特征函数乘以信号，就得到了输出的结果。我们用一个0Hz~Fs的chirp信号输入滤波器来测试，这个chirp信号的频谱就是一个矩形，得到的结果见下图

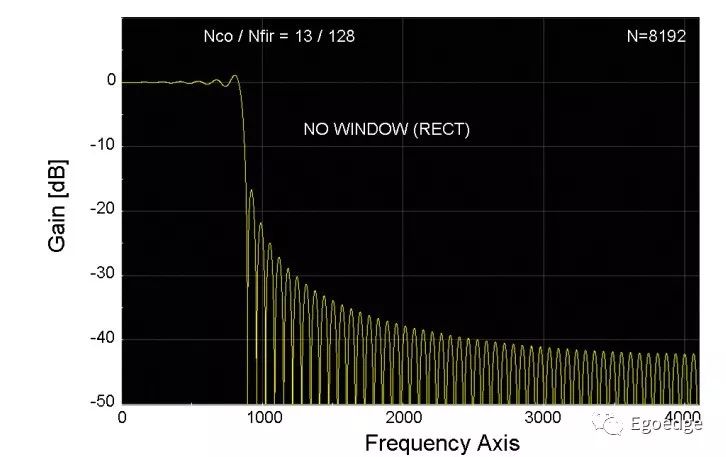
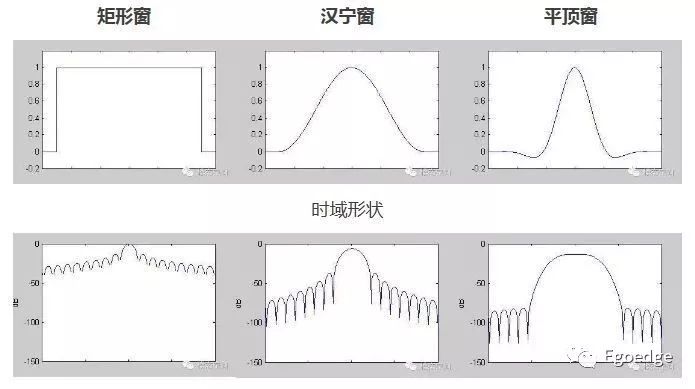
可以看到128阶FIR滤波器的边沿还是非常陡的，有很好的滤波性能，但旁瓣的抑制很差，这个就是FIR滤波器在频谱上的泄露。泄露是由于FFT只能处理有限时间长度的时域信号，如果时域截取的数据不是信号周期的整数倍，就会存在泄露。由于矩形窗的边沿过于陡，只有很小的概率正好截取到信号周期的整数倍，因此泄露很严重。可以通过选择合适的窗函数，来减少频谱上发生的泄露。一般常用的窗函数有矩形窗、汉宁窗和平顶窗，他们的特征如下图所示

不同窗函数所对应的结果看下图

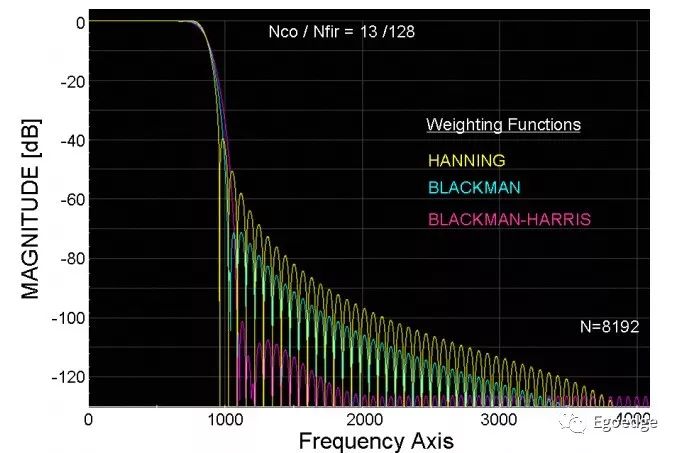
关于窗函数就不再介绍了，窗函数的选择是FIR滤波器设计的重点，矩形窗的优点在于计算量小，其他的窗函数基本都是基于升余弦函数，汉宁窗属于升余弦函数的一个特例。有兴趣的大家自己可以去研究研究。

最后要说的一点是，FIR滤波器的阶数越高，则边沿越陡，运算量越大。