支持向量机算法

1、支持向量机

1、基于统计理论的学习系统

2、属于有监督学习的方法

3、用于样本分类

4、分为线性分类模型与非线性分类模型

    下面看一道例题：有18组数据，有不同的类别属性，建立SVM模型。

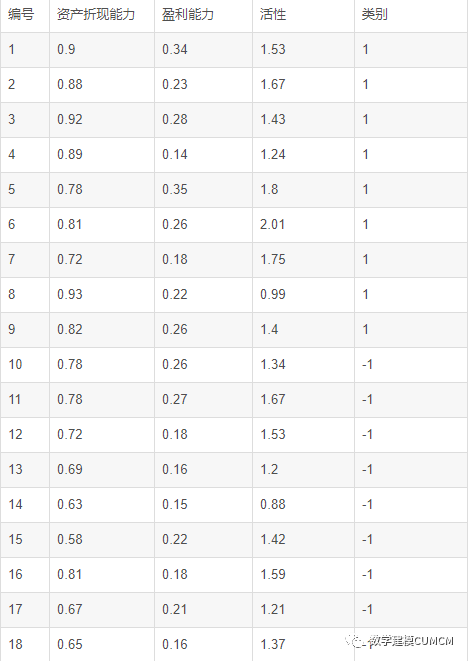
clear
clc
X0=xlsread('Excel文件位置','B2:E19');
for i=1:3
    X(:,i)=(X0(:,i)-mean(X0(:,i)))/std(X0(:,i));%数据标准化
end
[m,n]=size(X);
e=ones(m,1);
D=[X0(:,4)];
B=zeros(m,m);
C=zeros(m,m);
for i=1:m
    B(i,i)=1;
    C(i,i)=D(i,1);
end
A=[-X(:,1).*D,-X(:,2).*D,-X(:,3).*D,D,-B];
b=-e;
f=[0,0,0,0,ones(1,m)];
lb=[-inf,-inf,-inf,-inf,zeros(1,m)]';
x=linprog(f,A,b,[],[],lb);
W=[x(1,1),x(2,1),x(3,1)];
CC=x(4,1);
X1=[X(:,1),X(:,2),X(:,3)];
R1=X1*W'-CC;
R2=sign(R1);
disp('程序输出结果:');
disp('超平面方程为:');
disp(['X1:',num2str(x(1,1))]);
disp(['X2:',num2str(x(2,1))]);
disp(['X3:',num2str(x(3,1))]);
disp(['intercept:',num2str(x(4,1))]);
disp('超平面分类结果:');
R=[R1,R2]

结果展示：

Optimization terminated.
程序输出结果:
超平面方程为:
X1:2.4476
X2:0.07549
X3:1.17
intercept:0.70991

超平面分类结果:

R =

    2.6679    1.0000
    2.6442    1.0000
    2.6488    1.0000
    1.0000    1.0000
    1.0000    1.0000
    2.4507    1.0000
   -0.8074   -1.0000
    1.0000    1.0000
    0.1764    1.0000
   -1.0000   -1.0000
    0.3683    1.0000
   -1.7115   -1.0000
   -3.7894   -1.0000
   -6.5114   -1.0000
   -5.3694   -1.0000
    0.6273    1.0000
   -4.1523   -1.0000
   -4.0207   -1.0000

从结果可以看出存在一定的误差，例如，第16组数据分类为1。

审核编辑：刘清