本振相噪对发射信号的EVM有影响？

发射机中的本振相噪，是影响发射信号EVM的一个因素。

先来看看理论分析。

首先来看看EVM的定义。

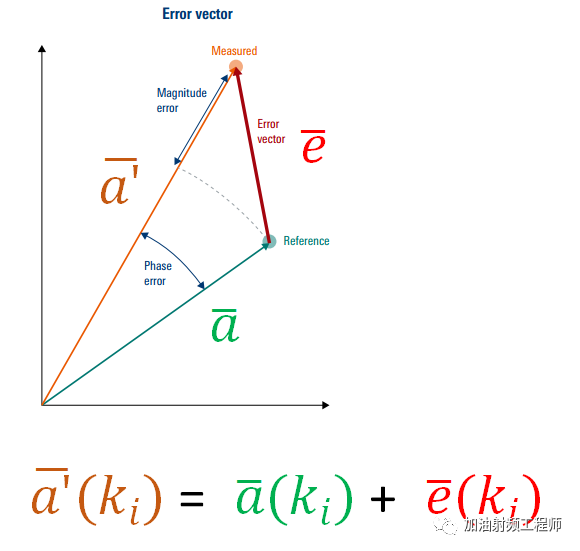
对于每一个符号而言，有一个理论上的位置，即上图中的绿点(Reference)，但是实际上，符号对应的点，在星座图上会有偏移，如上图中的桔黄色的点(Measured)。

而理想和现实之间的差距，即是误差矢量，如上图红色箭头所示。

由上图可知，对于每一个符号ki, 误差矢量可以由下式进行表示：

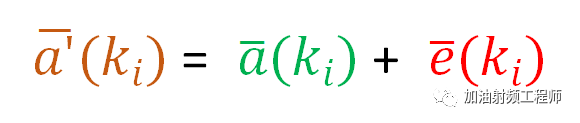
在文献[1]中，对EVM的定义是这样的：

我的理解是这样的，就是，虽然针对单个符号可以计算EVM，但是书中的定义，是基于多个符号对应误差矢量的平均值。

其数学表达式为：

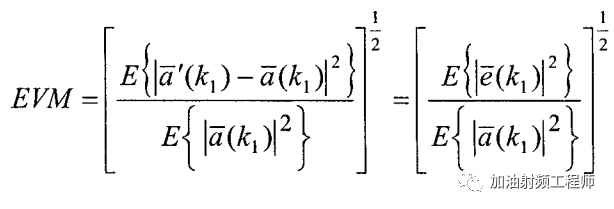
然后再看看怎么把相位噪声换算到EVM上。

既然，现在只是考虑相位噪声对EVM的影响，所以可以不考虑幅度误差。

并且，假设上述的矢量误差，是由于本振的相噪引起的。

本振的相噪，可以看成是一个很小的随机相位量，定义为：

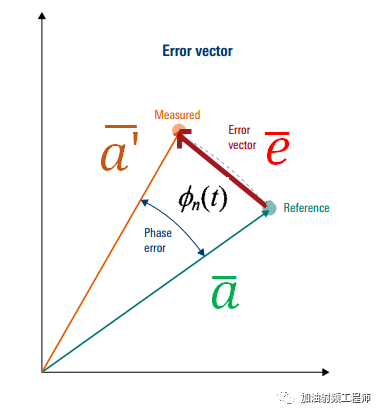
所以，实测的信号，可以用下式进行表示：

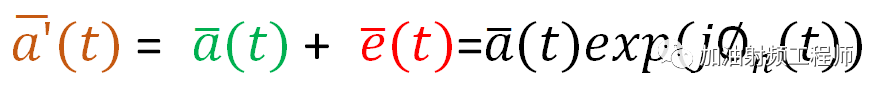
因此，误差矢量的幅度如下图所示：

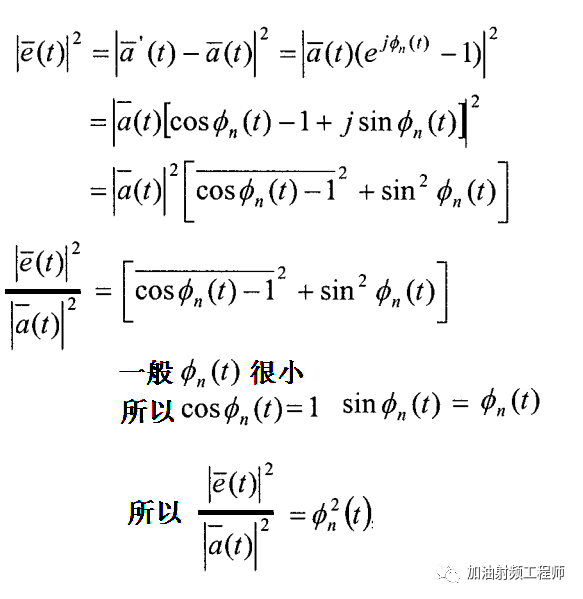
相噪的自相关函数与其对应的功率谱密度有如下的关系(我随机过程学的不好，所以下面的式子，并不是很理解，先copy过来)。

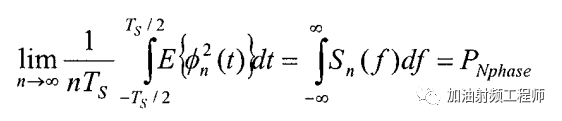
所以（在文献[1]的基础上，补了个dt，还有绿圈中为啥又不是Ts了呢？不过可以先看结论）:

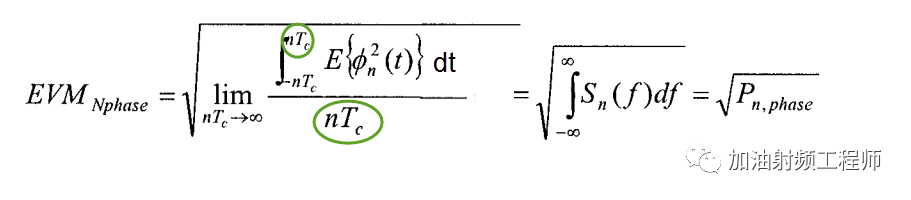
假设本振的环路带宽相对较宽，则由于相噪累积出来的能量为：

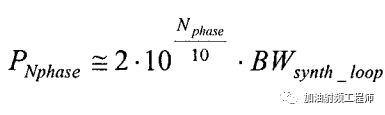
其中，Nphse是平均相噪，单位为dBc/Hz，BWsynth_loop是环路滤波器的带宽，单位为Hz。

所以，

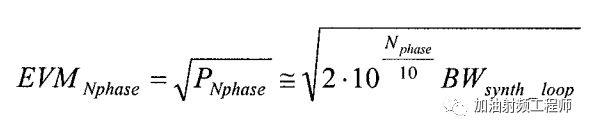
如果使用了多个本振，则

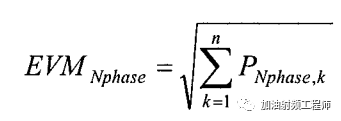
然后再看看仿真验证。

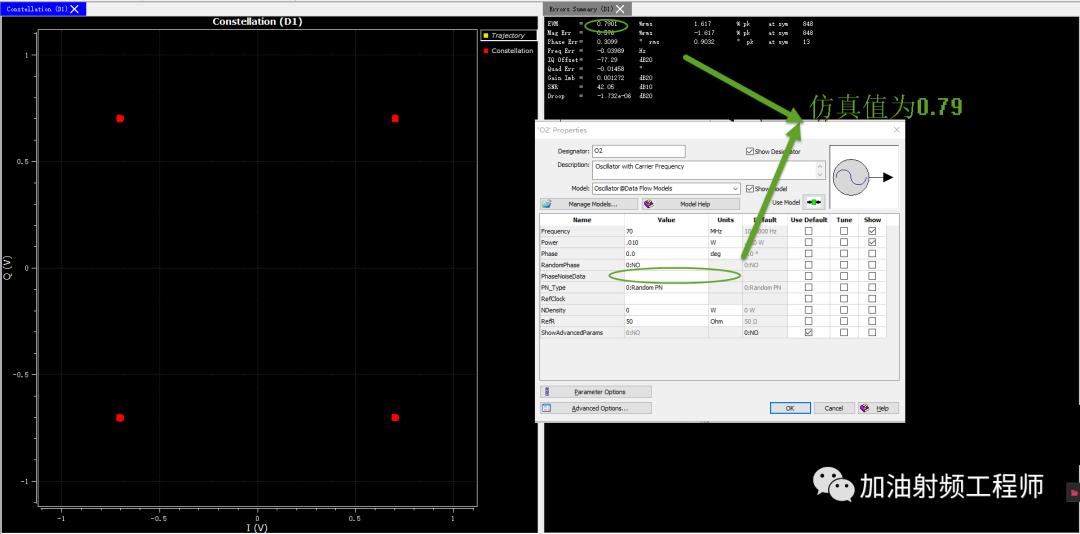
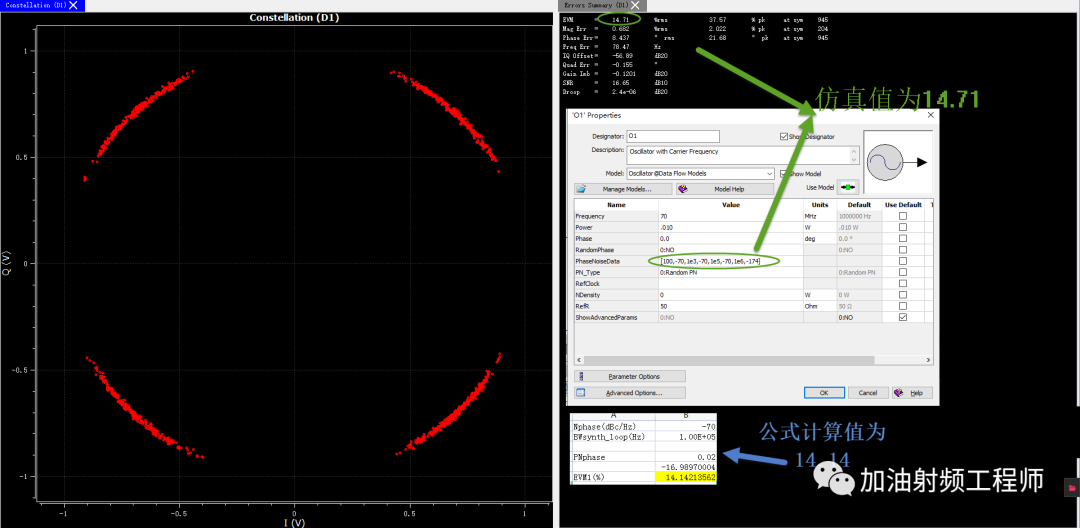
用SystemVue进行验证，发现当LO不考虑相噪时，EVM为0.79%。

当相噪为:

-70dBc/Hz@100Hz,

-70dBc/Hz@1000Hz

-70dBc/Hz@100KHz

-174dBc/Hz@1MHz

时，仿真得到的值为14.71%，而根据上述公式，计算得到的值为14.14%。两种结果对比来看，理论公式的预估还是比较准确的。

同时，可以从星座图中看到，测量点成为一个弧形，这也与开头的假设相呼应，即没有幅度误差或者很小，只有相位误差。

审核编辑：刘清