

电子说
初探卡尔曼滤波的广泛应用
卡尔曼滤波是基于线性系统的基础上,测量方差已知的前提下,在包含一系列噪声的观测数据中进行系统状态的最优估计,得到误差最小的估计值。
众所周知该方法经久不衰几十年,涉及领域包括机器人导航、运动控制、传感器融合、图像处理等。仅在无人驾驶中,我们就多处看到它的身影,比如:
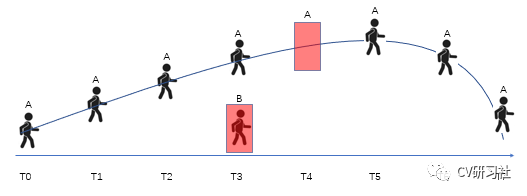
以感知中目标跟踪为例,卡尔曼滤波可以用来预测下一时刻行人运动的最优位置,不仅可以滤除检测带来的虚警,还可以弥补偶发的漏检,使目标的运动过程更加平滑。如下图所示:从T0到T7时刻,检测器对行人A的观测结果大部分是良好的,但是在T3时刻出现了虚警B,此时卡尔曼滤波器会根据T3的前后时刻来判断行人B是一个新的对象还是噪声;在T4时刻检测器再次失效,行人A消失了,此时卡尔曼滤波器会根据T3时刻行人A的位置来估计T4时刻A可能运动到某处作为结果。
既然线性系统是卡尔曼滤波的前提,那么为何它还能如此广泛应用?
以车辆运动模型为例,虽然在整个运动过程中很难拟合出其运动规律,但是如果把每次运动的时间间隔都缩的很小,那么就可以近似的将车辆的运动看成匀速、匀加速、均减速等。
入门卡尔曼滤波的基本原理
卡尔曼滤波器采用递归的方式来解决线性问题,只需上一个时刻的估计值和当前的测量值来进行状态估计,并使估计均方误差最小。作为初步理解,我们只需要看下面两个方程:
预测方程如下所示:

其中A是状态转移矩阵,用来表达如何将上一时刻的状态量通过某种关系转换成当前状态;B是控制输入矩阵,但是在实际应用中这一项通常为0;w表示的过程噪声,是期望为0,方程为Q的高斯白噪声。
观测方程如下所示:

很多初学者会对观测方程产生疑问,为什么它可以由状态值和观测误差来表示?观测量不是指传感器直接输出吗?
其实它是对传感器测量的模拟仿真,用真值加上误差来表征传感器的测量值,而H可以看成是状态量到观测量的一种变换关系。我们将状态变换过程和模拟的观测过程合起来就是下面的流程图:

因此使用卡尔曼滤波器解决实际问题,就需要满足两大基本假设:
进阶卡尔曼滤波的公式推演
卡尔曼滤波过程有五大核心公式,手撸版本如下:公式(1)(2)属于预测过程,公式(3)(4)(5)属于状态更新。我们一条条来解释这几个公式:

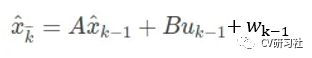
上式是先验估计的求解过程:由上一时刻的最优估计值结合控制输入和环境噪声来预测当前的状态估计值。在很多时候该公式会被简化成当前估计值等于上一时刻最优估计+噪声,在目标跟踪任务中BU项是可以被忽略的,A表示的是状态转移矩阵或者说是运动模型,如何准确的构建状态矩阵需要用户结合自身场景来确定。所以像EKF,UKF等并非从算法上对KF做了什么优化,而是搭建更合适的运动模型来模拟实际场景。

上式是先验估计的协方差求解过程:由上一时刻的先验估计协方差P和过程噪声Q决定(推导的过程可以对公式(1)的当前估计值求取协方差即可得到)。这里我们会发现先验估计协方差P中是包含过程噪声Q的,所以当P越小会导致卡尔曼增益K就越小(这里需要结合卡尔曼增益K的公式一起看)。

上式是更新卡尔曼增益的过程:它其实是一个中间变量,我们在说先验估计协方差P的时候提到,P中是包括过程噪声Q的,那么结合该式可以发现卡尔曼增益K的调节本质上就是调节Q和R两个噪声值。

上式是最优估计的修正过程:这里Z是我们的观测值,X相当于我们的预测值,直接拿观测值和预测值做差,用K来决定是相信观测值Z多一些还是相信预测值X多一些。
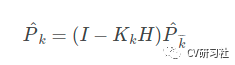
上式是更新后验估计的协方差过程:主要用于下一次迭代的输入,属于一个中间变量,一旦P0这个初始值确定后,该值会慢慢趋于收敛(通过调Q)。算法调优时可以不用特别关注该项。
深入卡尔曼滤波的参数调优
卡尔曼滤波是一个需要手动调参的算法,在上面的介绍中我们提到最优估计值是先验估计和观测值之间的权衡,而这个权重是通过卡尔曼增益K进行调节的。通过K的推导公式可以发现它的大小取决于超参数Q和R。
回顾一下上一节公式中的Q和R是什么?
在卡尔曼滤波的过程中有两种噪声,过程噪声和观测噪声:
它们均符合正态分布,Q就是过程噪声的方差,Q值越小表示对预测值的信任度越高,但是过小的Q也会引起系统发散;Q值越大表示对测量值的信任度就会变高。
R是观测噪声的方差,R值越小表示系统的初始增益大,收敛快更快,但是在稳态情况下引入过多的噪声容易出现震荡不收敛的现象;R值越大表示对测量值的信任度降低,响应也会随着变慢。
另一个超参数就是P的初始值,它决定了滤波器初始的工作状态,更准确的说就是滤波器初始的收敛速度。调大P0能够迭代出较大的初始增益,相应的使滤波器更快的响应输入信号的变化。
所以卡尔曼滤波调参是在P0,Q,R之间追求系统和滤波之前的收敛平衡。对于初学者而言,通常不太关心P0,只需不为0即可;而Q和R需要一点点尝试,适当的增加/减小参数,反复迭代才能逐步收敛于一个稳定值。
实践卡尔曼滤波的目标跟踪
多目标跟踪有很多方法,可以使用当前帧和之前帧中的信息做当前时刻的目标跟踪;也可以对每一帧的预测使用所有帧中的信息寻找全局最优。
这里我们基于卡尔曼滤波算法将运动模型看似线性匀速运动来估计帧间位移,并结合匈牙利算法进行预测的外接框和检测的外接框做数据匹配,最终选择合适的目标外接框作为最优跟踪BBox。应用于图像空间需要以下几步:
估计模型
这里我们采用卡尔曼滤波对目标的轨迹进行预测,并且使用置信度较高的跟踪结果进行预测的修正。
数据关联
这里我们采用带权重的匈牙利算法,使用IoU构建的权重作为成本矩阵,当然这里的权重还可以以不同维度的特征做加权。
实验例子
下面是一个基于C++实现的检测+跟踪的例子,直接原生的算法未做任何优化,所以并非工程可用,但也更能暴露算法本身的缺陷,从而加以针对性的优化策略。从视频中我们可以看到基于卡尔曼滤波+数据关联的跟踪算法对独立目标具有稳定的输出,但是当目标较远时或者存在遮挡的情况下,id就会发生漂移。我们可以从以下三个方面来分析:
全部0条评论

快来发表一下你的评论吧 !
