浅析基于差分扩展的可逆水印算法

一、差分扩展

数字水印已经逐渐成为了一种有效的版权保护手段，它通过嵌入几乎不可感知的水印信号到图像、音频、视频数据中来保护这些媒体文件的版权不被非法利用、来认证来源或者增强其价值。水印化前后的作品之间的失真通常在视觉上是不可感知。但在一些特殊场合，即使是这些无法被感知的失真也是不能容忍的。因此就出现了可逆水印，其要求不能能抽取出水印，还能够无损的将水印化作品恢复成原来的作品。

早期的可逆水印算法都是基于算数模的加法扩频水印算法；另一种可逆水印是对图像的某些特征进行无损压缩，然后将水印加入由压缩所留出来的空间中以达到可逆的目的。而基于差分扩展的可逆水印是通过对一对像素值的差值进行扩展来进行可逆变换的水印算法。该算法的主体思想是对相邻两个像素值的差值进行扩展或变换形成新的像素对以达到水印嵌入的目的，然后再从新的像素对的差值反变换即可还原出原始图像和嵌入的水印。为了保证不可察觉性和图像的质量，该算法将所有的像素对分为可扩展的、可改变的及不可改变的这三种类型，其中可扩展的也一定是可改变的。而只有可扩展的和可改变的像素对可以用于数字水印的嵌入。该算法的特点在于通过利用相邻两个像素对的差在不需要增加存储空间消耗的情况下，将数字水印的信息码流不可察觉的嵌入到载体图像中；然后在通过相似的方法将嵌入的信息码流从载体图像中提取出来并将载体图像无损的恢复以达到完整和可逆的效果。

为了更好的理解差分扩展的变换和还原，这里我们举个例子：假设有一对像素对(x, y)，其中x=206，y=201.我们想要嵌入的信息比特b=1.那么这个像素对的平均值l和差h为：

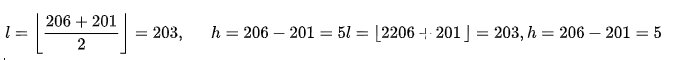
我们把b添加到到h的二进制表示1012的最低有效位(LSB)中得到了一个新差h’=10112=11.用数学表达为：

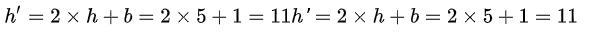
最后根据这个新差可以得到这个像素对的新值作为嵌入之后的像素值：

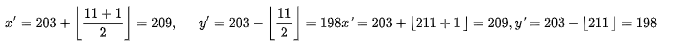
通过以上的这些步骤我们可以得到嵌入信息之后的像素对(x’, y’). 如果我们想要恢复原始的像素对和嵌入的信息，我们可以根据上述公式再次计算嵌入信息之后像素对的平均值l’和差h’：

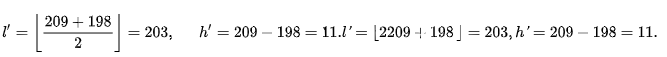
根据上述公式得出的像素对差h’可以计算出嵌入的信息b及原始的像素对差：

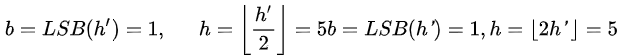
从公式(4)中和公式(5)中得到的l’和h就能恢复出原始的像素对：

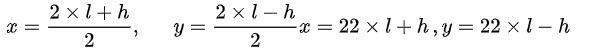
在这个例子中我们将信息比特b嵌入到像素对差h的最低有效位上使得h的位数从三位扩展到四位，这种可逆信息嵌入的操作就叫做差分扩展(DE).

二、可逆数据转换及限制

从1中我们可以了解到差分扩展的一些基本操作，不难想到可以将这种操作扩展到可逆水印的算法中。对于一副8比特的灰度图像来说，其所包含的像素对可以得出它们的平均值l和差h为：

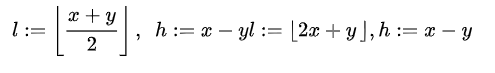
其反变换为：

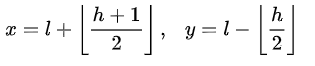
由于x,y的区间范围是[0, 255]，因此我们有:

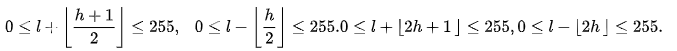
当使用差分扩展将一个信息比特b嵌入到差值h中时，新的、可被扩展的差值h’将变成：

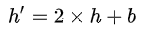
为了避免像素对超出取值范围，也即溢出，h’必须满足以下条件:

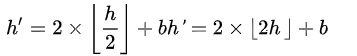
满足上述条件的像素对的差称之为可扩展的，因为该像素对可以使用差分扩展进行信息的嵌入且不会导致数据的溢出。由此同时，我们也可以不对像素值的差进行差分扩展，而是改为对其最低有效位进行直接修改。通过将其最低有效位直接修改成信息比特也可以达到信息嵌入的目的。这时的新差h’为:

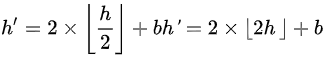
同时为了满足嵌入之后的数据不发生溢出，h’也必须满足以下条件:

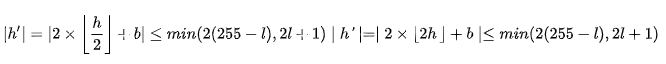
满足上述条件的像素对的差称之为可改变的，因为该像素对可以使用直接修改的方法进行信息的嵌入且不会导致数据的溢出。不难得出，可拓展的和可改变的像素值的差经过差分扩展或者直接修改后其新差仍然是可修改的，并且可扩展的差值一定也是可改变的。因此我们可以得出以下差值h的分类:

• 可扩展的差值h：可以对其最低有效位进行差分扩展而不会导致数据溢出。其应该满足：
  
• 可改变的差值h：可以对其最低有效位进行直接修改而不会导致数据溢出。其应该满足：
  
• 不可改变的差值h：既不可扩展也不可改变的差值h.

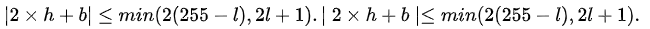
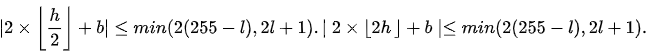
图1 差值h的分类

同时还可以发现当h=0或者-1时，可扩展条件和可改变条件是相同的。因此我们可以按照上述对差值h的分类将像素对分成四个集合：

• EZ：包含了差值h为0或-1的所有可扩展像素对。
• EN：包含了差值h不为0或者-1的所有可扩展像素对。
• CN：包含了不是可扩展像素对的所有可改变像素对。
• NC：包含了所有不可改变的像素对。

由上文可得EZ、EN、CN是可以嵌入信息的像素对，而NC是不可以嵌入信息的像素对。因此我们首先应该先将可嵌入信息的像素对找出来形成一个location map信息集。并且为了无损的恢复出原始图像，我们也应该记录下可改变差值的那些被直接修改掉的最低有效位信息并形成一个最低有效位信息集。Location map信息集(L)、最低有效位信息集(C)以及想要嵌入的数字水印payload(P)共同构成了信息流(B)一并嵌入到了载体图像中完成了可逆水印的嵌入。为了保证数据被有效嵌入而不发生信息的溢出，其B的体积必须满足:

三、信息的嵌入和提取

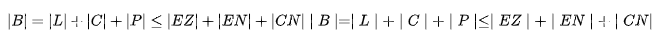
按照2所述的基于差分扩展的数字水印的知识，我们可以得到数据嵌入的步骤，该步骤如下所示：

1. 将原始载体图像分成一个像素对集合，再对每个像素对求平均值l和差值h。
2. 将差值h按照分类规则进行分组并形成四个不同的子集EZ、EN、CN、NC集，其中EN集还可以再分成EN1集(可二次扩展)和EN2集(不可二次扩展)。
3. 根据差值h四个不同子集的状态对图像的位置进行标记并形成location map信息集，再对该信息集进行压缩存储成L比特流。
4. 提取可改变差值h的最低有效位形成最低有效位集，然后再进行压缩储存形成C比特流。
5. 对有效负载(数字水印)进行压缩储存形成P比特流。
6. 将L、C、P比特流进行合并形成B比特流并按照差值h的状态进行差分扩展或修改LSB以完成数据嵌入。

这些数据嵌入的算法步骤的流程图如下所示：

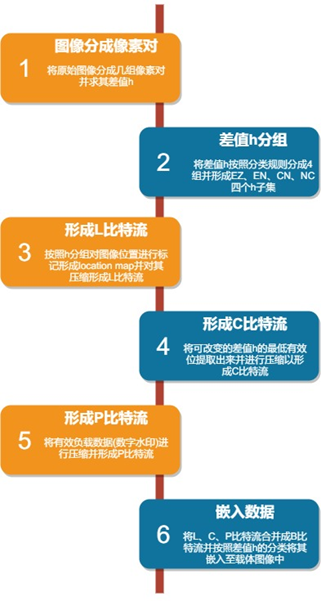
图2 基于差分扩展的水印嵌入的流程图

通过以上步骤我们可以将水印嵌入到载体图像上。如果我们想要提取出水印和复原出原始的图像，可以逆着上述步骤进行数据的提取即可得到水印和原始的图像。因此，其提取数据的方法和步骤如下所示：

1. 将新图像进行像素对分组并求新像素对的差值h’和平均值l.
2. 提取出差值h’的最低有效位形成B比特流并将L比特流分离出来。
3. 将L比特流进行解压还原成location map数据集。
4. 根据location map对差值h’进行筛选并分离出C比特流和P比特流。
5. 将P比特流进行解压缩后恢复出水印信息。
6. 将C比特流解压后得到的最低有效数据集并根据location map将其最低有效数据恢复到最低有效位上去。
7. 根据差值h’和location map恢复出原始的差值h，再根据差值h和平均值l得到原始的像素对数据并恢复出原始图像。

这些水印的提取和原始图像的恢复步骤可以用以下流程图表示(见图3)：

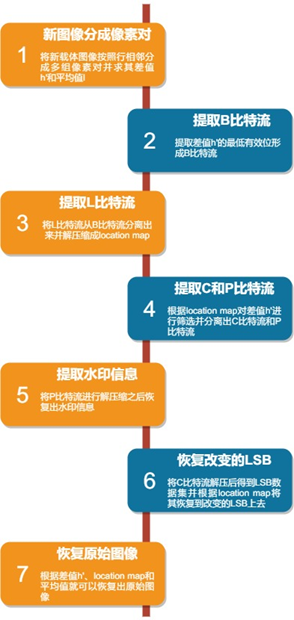
图3 基于差分扩展的水印提取的流程图