buck电路中的电感电流波形分析

1没有电容，a点的波形图

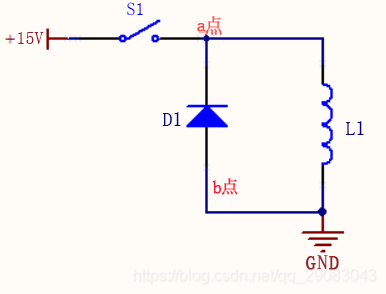
上图中，把所有器件都想象为理想状态下，开关S1闭合和断开的过程，流过L1的电流的波形是怎样的？

（1）开关闭合时，电流开始升高：

根据电感公式，得：电流变化率 = Vin / L = 15 / L。

（2）电路稳定时，也就是电流变化率为0，L1两端的电压为0.

（3）开关断开时，D1把电感两端的电压钳位在0.7V，因为b点为地，是0V，所以a点就是-0.7V；根据电感公式，得：电流变化率 = -0.7 / L。

从这里可以看出，上升的斜率比下降的斜率大，所以波形如下图所示：

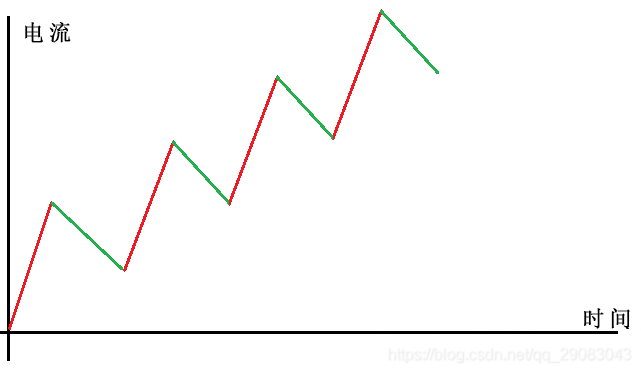
可以看出电流是失控的，会一直增大。只有当电流的上升频率和下降频率相同时，开关电源才能维持稳定的电压。

2有电容，a点的波形图

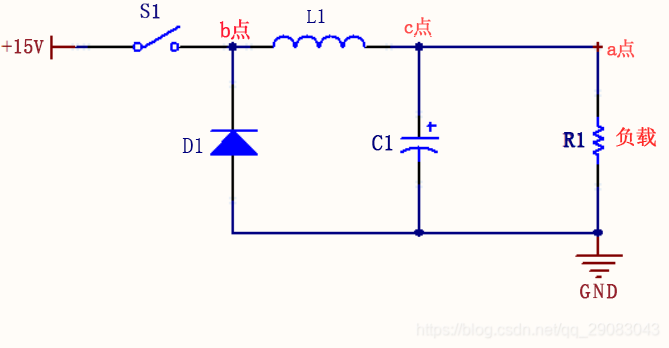
（1）导通瞬间，电流直接流过C1，负载被短路，相当于15V直接接在L1中，此时电流上升斜率 = 15 / L。如果此时断开开关，因为是突然断开，是高频信号，会直接将电容C1短路，所以电感两端的电压和D1两端的电压相等（二极管将电压钳位在0.7V）。电流下降斜率 = 0.7 / L。

（2）随着导通的进行，开始对C1充电，假设充电到2V。Vc为2V，那么电感两端电压为15 - 2 = 13V，此时电流上升斜率 = 13 / L。如果此时断开开关，C1两端电压为2V，二极管两端的电压为-0.7V，所以电感两端必须为2.7V，此时电流下降斜率 = 2.7 / L。

从这里可以看出，电感电流上升过程中，斜率逐渐变小，由最开始的15 / L，到后来的13 / L；电感电流下降过程中，斜率逐渐变大，由最开始的0.7V / L，到后来的2,7 / L。

通过上述分析（这里不好理解）：加了一个电容后，电感电流的上升斜率和下降斜率达到一个平衡（最终相等）。总之，上图所示的电路图，只要开关S1开和关的频率固定，a点电压几乎非常稳定。

3稳定a点电压的方法

只要起点和终点一样，a点电压就非常稳定。

（1）上升频率和下降频率相同，可以使输出稳定。

（2）上升频率比下降频率高，但下降时间更长。

（3）上升频率比下降频率低，但下降时间短。

4电感工作模式

因为电感是和负载串联的，所以电感上的电流大小就是负载中的电流大小。

（1）连续模式

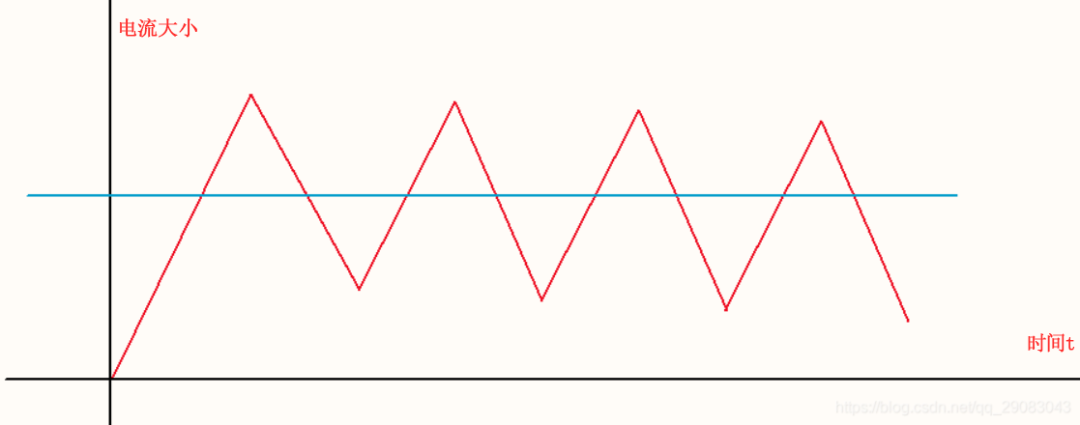
中间蓝色的线对应的电流值，就是电感输出的平均电流。电感电流的峰峰值都不为0，称为连续模式，也简称CCM。这种模式最常用。

（2）临界模式

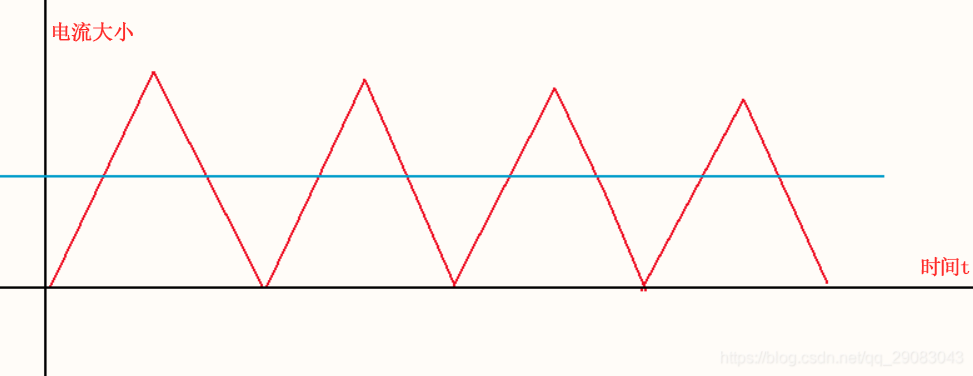
电流的下峰值为0，称为临界模式，因为是连续的，也可以称为临界连续模式，简称BCM。

（3）断续模式

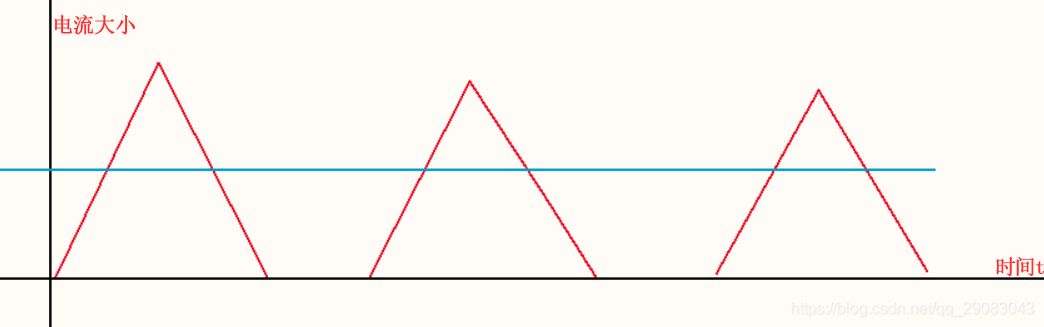
电流下降到0后，过一段时间电流才开始上升。也就是一个周期中，有一段时间电流为0，这种模式称为断续模式，简称DCM。

一般是让电感工作在连续模式，系统比较稳定。

5伏秒法

要怎样才能让系统输出稳定电压呢？也就是电感不会失控？只要保证以下公式成立即可：

上升的△V * △t = 下降的△V * △t

电流上升时电压的变化量 * 时间 = 电流下降时电压的变化量 * 时间，开通时电压和时间的积分要和关断时候的积分相等。因为是电压乘以时间，所以被称为伏秒法。

只要红色的面积和绿色的面积相等，就能保证电感输出稳定的电流。

当时大多数情况下，上升的△V和下降的△V不相等，所以需要调节开关的导通和关断时间，让两者和时间相乘后相等，乘积相等即可，满足伏秒法则，电感工作就比较稳定。

6总结

（1）感应电压的大小与电流的大小无关，只和电流的变化率有关。

（2）对于buck电路而言，因为电感和负载串联，所以电感的电流和负载电流相同，并且因为流过电感的电流是有纹波的，所以这里说的是电感的平均电流。

（3）对于连续工作模式下的电感，电感的平均电流位于电流波形图的几何中心，也就是下图的蓝色部分。

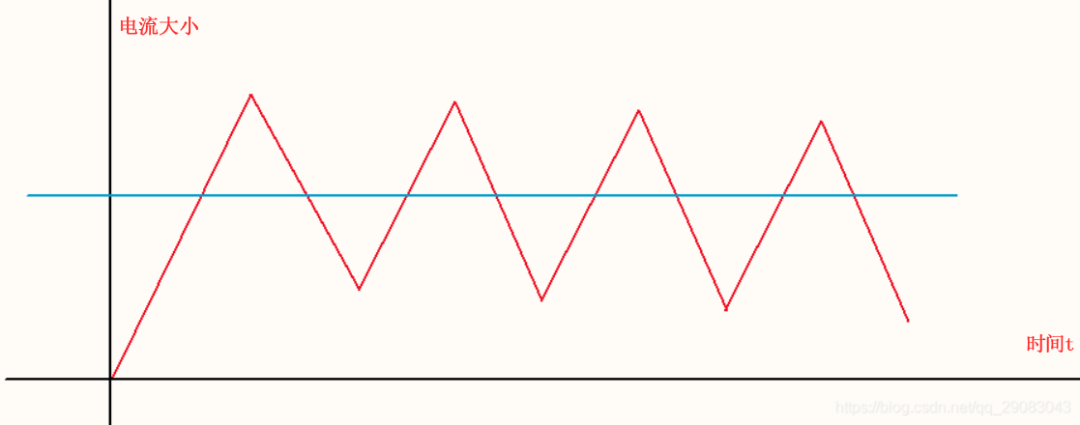
本文来源：CSDN博主开继电子

审核编辑：汤梓红