纯电感电路中电流与电压的相位关系

由电阻很小的电感线圈组成的交流电路，都可近似地看成是纯电感电路。如下图a所示为由一个线圈构成的纯电感电路。

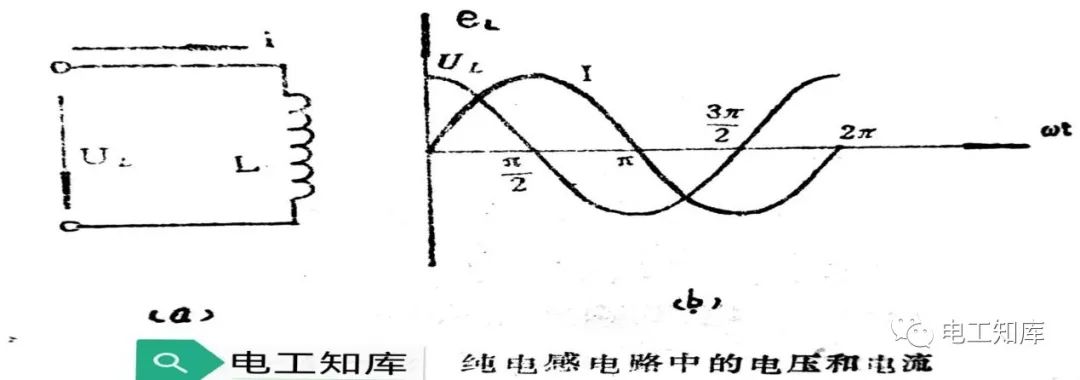
1、纯电感电路中电流与电压的相位关系

在纯电感线圈的两端，加上交流电压u L ，线圈中必定要产生一交流电流i，由于这一电流时刻都在变化，因而线圈上就产生自感电动势来反抗电流的改变，因而线圈中的电流变化就要落后于线圈两端的电压变化，uL和i之间就会有相位差。

对于一个内阻很小的电源，其电动势与端电压总是大小相等方向相反，因而:

u L =-e L =-(-L∆i/∆t)=L∆i/∆t

由上式可以看出，线圈两端的电压大小与电流的变化率成正比。下面就通过上式来分析电流与电压之间的相位关系。

设线圈中电流的初相位为零。电流波形如上图b所示。现把一个周期电流的变化分成四个阶段来讨论:

在0π/2,即第一个1/4周期内，电流从零增加到最大正值。此间电流的变化率∆i/∆t为正值,并且起始时最大，然后逐渐减小到零。根据uL~=L∆i/∆t可知，此期间的电压uL从最大值逐渐变为零。

在π/2π,即第二个1/4周期内，电流从最大值减小到零。此间电流的变化率∆i/∆t为负值,并且从零变到最大负值。uL~也从零变到最大负值。

在π3π/2,即第三个1/4周期内，电流从零变为最大负值，此间电流的变化率仍为负值,且从最大负值变到零，则uL~也从最大负值变到零。

在3π/22π,即第四个1/4周期内，电流从最大负值变到零，此间电流的变化率为正值,且从零变到最大正值，则uL~也从零变到最大正值。

从以上分析可得上图b所示的uL的波形图。从波形图可清楚地看出：在纯电感线圈中的正弦电流要比它两端的电压滞后90°。即电压总是超前电流90°。这就是纯电感电路中电流和电压的相位关系。

设流过电感的正弦电流的初相位为零，则电流、电压的瞬时值表达式为:

i=Imsinωt

u L =ULsin(ωt+π/2)

2、纯电感电路中电流与电压的数量关系

由数学推导可知，电压的最大值为：

U Lm =ωLIm

若把两边同除以√2，则得:

U L =ωLI或I=U~L~/ωL=U~L~/X~L~

式中X L =ωL=2πfL

XL称为电感抗，简称感抗，它的单位是欧姆。因此，电感线圈中的电流有效值就等于线圈两端电压的有效值除以它的感抗。

感抗是用来表示电感线圈对交流阻碍作用的一个物理量。感抗的大小，取决于线圈的电感量L和流过它的电流频率f。对具有某一电感量的线圈而言，f越高则XL越大。在相同电压作用下，线圈中的电流就会减小。在直流电路中，因频率f=0，故线圈的感抗也等于零，这时线圈只起电阻作用。由于一般线圈的电阻很小，故电感线圈可视为短路。

3、纯电感电路的功率

纯电感线圈的瞬时功率为:

P L =uLi

=UL~~msin(ωt+π/2)ILmsinωt

=ULmImsinωtcosωt

=ULmImsin2ωt/2

=ULIsin2ωt

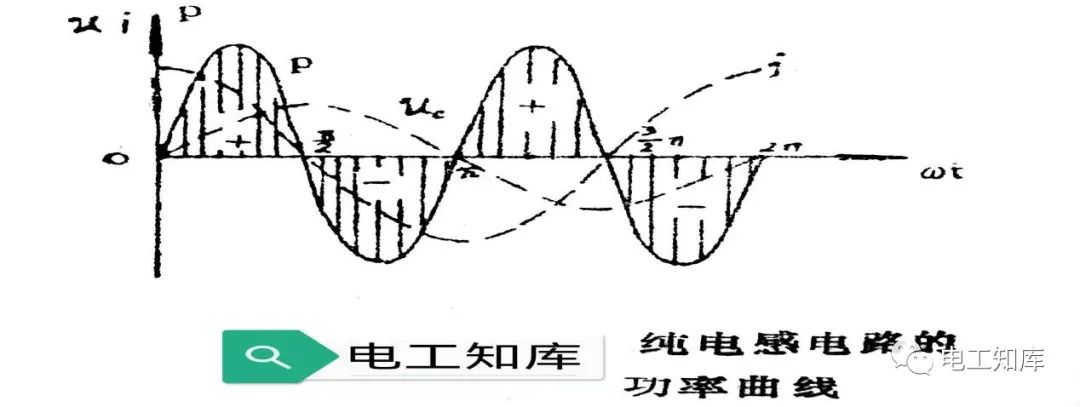
上图画出了PL的变化曲线，从图中可以看到，在第一和第三个1/4周期内，PL是正值，这就表示线圈要从电源方面吸取电能并把它转换为电磁能，储藏在线圈周围的磁场中，此时线圈起着一个负载的作用。但在第二和第四个1/4周期内，PL为负值，这表示线圈是向电源输送能量。即线图把磁能再转换为电能而送回电源，此时线圈起着一个电源的作用。综上所述，纯电感线圈时而“吞进”功率，时而“吐出”功率，在一个周期内的平均功率为零，平均功率不能反映线圈能量交换的规模，因而就用瞬时功率的最大值来反映这种能量交换的规模，并把它叫做电路的无功功率。无功功率用字母QL表示。QL的大小为：

Q L =ULI=I^2^X~L~=U~L~^2^/X~L~

为与有功功率相区别，无功功率的单位是乏。在上式中，当各物理量的单位分别用伏特、安培、欧姆时，无功功率的单位是乏（var）。

必须指出，“无功”的含义是“交换”而不是“消耗”，它是相对“有功”而言的，绝不能理解为“无用”。