基于碰撞电离率模型的Miller公式S参数拟合分析

我们应用简单的Fulop模型对平行平面结进行了分析，对复杂的Chynoweth模型进行了化简，由化简的公式可得碰撞电离率积分和外加电压之间存在一定的关系。

这一关系通常可以用Miller公式 ^[38]^ 表征，即：

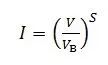(1)

其中的I为碰撞电离率积分，V为外加电压，VB为结的击穿电压，S为Miller常数。

在设计器件时，耐压设计是很重要的一环。这关系到耐压区掺杂，厚度等一系列问题。Miller公式可以用于判断开基区晶体管或Shockley二极管的正向阻断电压。Miller公式中S参数与掺杂浓度存在着密切关系。

此次，我们将基于已有的Miller公式，应用MATLAB对不同漂移区掺杂浓度下的S参数进行确定，提出参数S与漂移区掺杂浓度N的拟合公式，并验证其准确性。

此处依然采用MEDICI中的准确的Chynoweth模型对碰撞电离率积分进行提取：

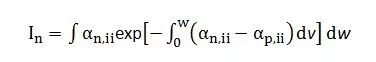(2)

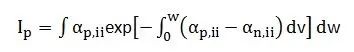(3)

因此碰撞电离积分可表示为：

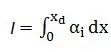
当电压达到雪崩击穿电压时，电流急剧上升，势垒区流出的载流子电流远远大于流进的载流子电流，二者的比值称为雪崩倍增因子，用符号M来表示。

经计算M与碰撞电离率之间关系为

：

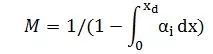
当发生雪崩击穿时，M趋向于无穷大，则I等于1，即碰撞电离率积分等于1时的外加电压就是所谓的雪崩击穿电压VB。此时势垒区对应的最大电场为击穿电场E c 。

可以采用extract语句在MEDICI对碰撞电离率积分进行提取。

结果下图1所示：

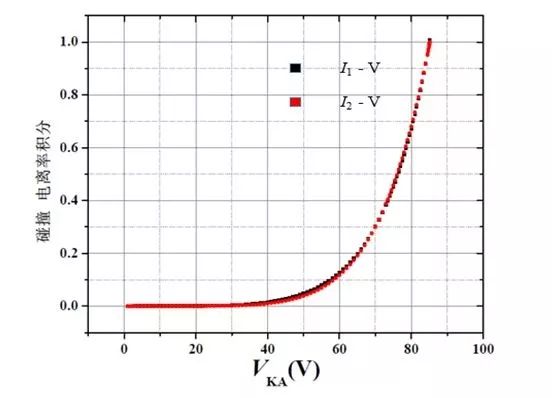
图1 碰撞电离率积分与外加电压的关系图

从图1中可以看出拟合出的碰撞电离率积分与外加电压的关系曲线（红色曲线）与提取出的碰撞电离率积分与外加电压关系曲线图（黑色曲线）几乎完全重合。

具体结果如表1所示：

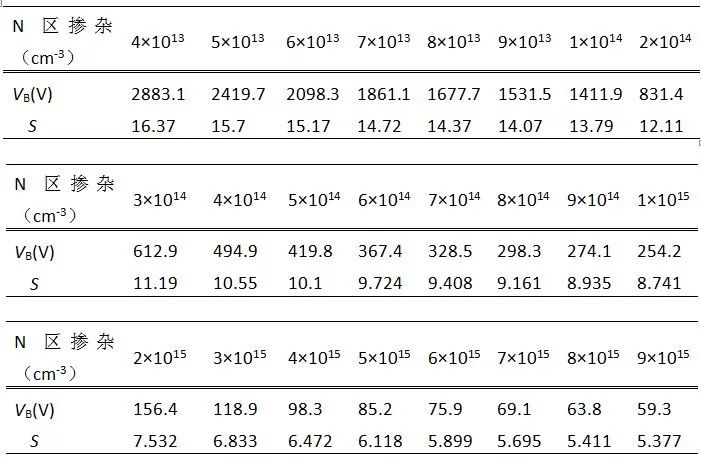
表1.不同浓度下的击穿电压和S值

从表1中可以看出随着N区掺杂浓度的变大，击穿电压和S值逐步下降。

得到了如下两个关系式：

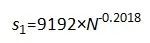(4)

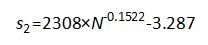(5)

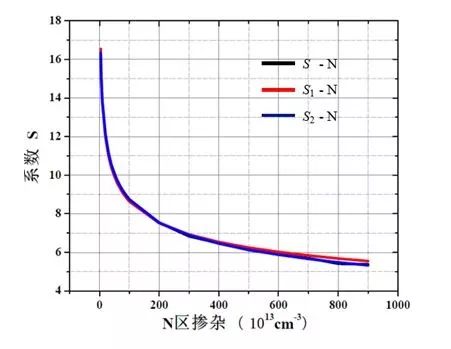
图2 拟合曲线与真实曲线的比较

本文阐述了雪崩击穿电压与轻掺杂区浓度变化的关系，对碰撞电离率积分与外加偏压的关系和Miller公式中S参数与轻掺杂区浓度的关系应用MATLAB进行了拟合，得到了近似的I-V表达式，S-N表达式，并对这些表达式进行了准确性的验证。

这种关系的确定，对分析开基区晶体管或晶闸管（如Shockley二极管）的正向阻断电压时有一定的借鉴意义。