

机器学习与线性回归
或许我们所有人都会学习的第一个机器学习算法就是线性回归算法,它无疑是最基本且被广泛使用的技术之一——尤其是在预测分析方面。
线性回归的主要优势在于其简单性,可以相当容易地实施。而简单意味着该算法也具有很高的可解释性。
本质上,线性回归试图通过将线性方程拟合到观测数据点来对给定数据集进行建模。
因此,这里的关键概念是线性。假设我们的特征(可以是一个或多个)与某个目标对象之间存在线性关系。
这种线性可以通过以下形式的方程表示:
y = β0 + β1x1 + β2x2 + ... + βn*xn + ε
其中:
y 是因变量(我们试图预测的结果)。
x1, x2, ..., xn 是自变量(预测因子)。
β0, β1, ..., βn 是系数,代表每个预测因子与因变量之间的量化关系。
ε 是误差项,用于解释 y 中未被 x 变量解释的变异性。
线性回归模型的目标是以这样一种方式估计这些系数,即最小化残差(观测值 (y) 与模型预测值之间的差异)。
线性回归在建模计数的局限性
计数数据的本质
计数数据指的是代表事件发生次数或发生数量的数据——呼叫中心接收的电话数量或商店的销售交易数量。
这类数据本质上是离散的且非负的。
线性回归在处理计数数据时的不足
尽管线性回归应用广泛,但在应用于计数数据时面临某些局限性:
负数预测问题
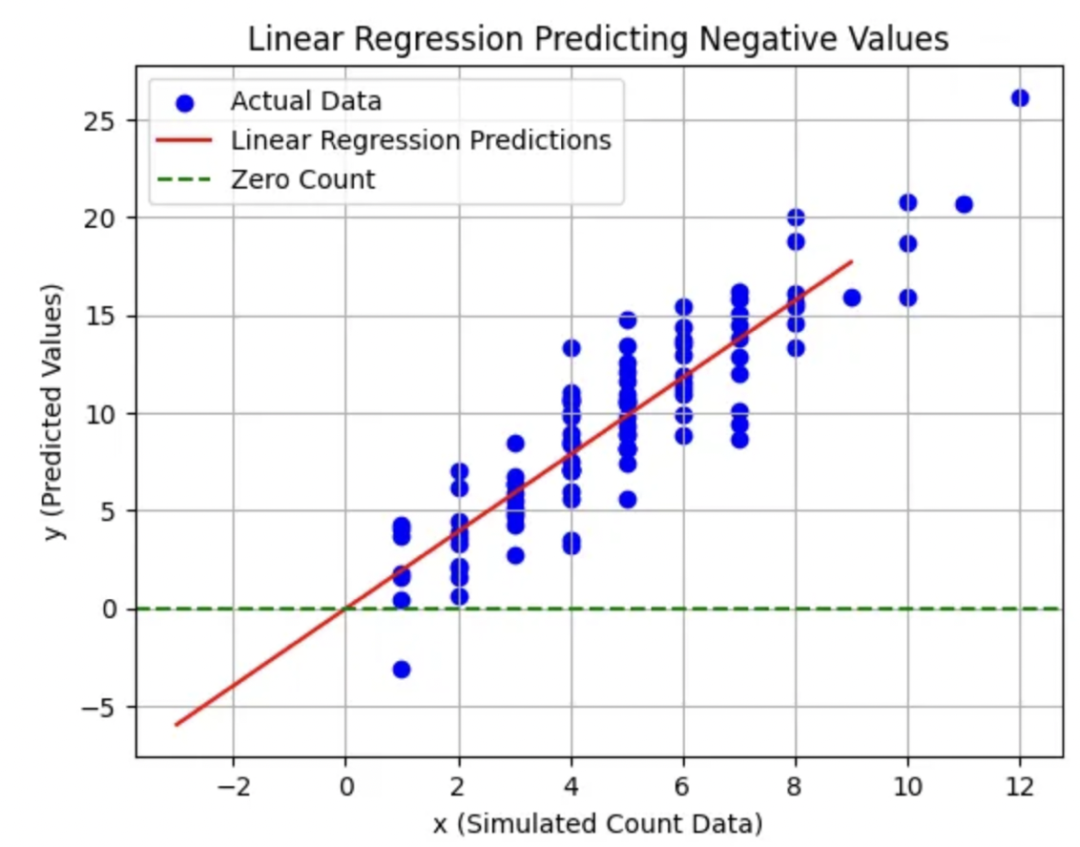
线性回归有时可能会为计数数据预测出负数值,这在现实世界场景中是不合理的。
这是将线性回归应用于非负计数数据时的一个根本性缺陷。
例如,预测“-2个电话接听”是不合理的。
考虑下面的例子:
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import LinearRegression
# Simulating count data
np.random.seed(0)
x = np.random.poisson(5, 100) # Simulating count data with a Poisson distribution
y = 2 * x + np.random.normal(0, 2, 100) # Adding some noise
# Linear Regression Model
model = LinearRegression()
model.fit(x.reshape(-1, 1), y)
# Predictions including negative values
x_test = np.array(range(-3, 10)) # Including negative values to illustrate the issue
y_pred = model.predict(x_test.reshape(-1, 1))
# Plotting
plt.scatter(x, y, color='blue', label='Actual Data')
plt.plot(x_test, y_pred, color='red', label='Linear Regression Predictions')
plt.axhline(0, color='green', linestyle='--', label='Zero Count')
plt.xlabel('x (Simulated Count Data)')
plt.ylabel('y (Predicted Values)')
plt.title('Linear Regression Predicting Negative Values')
plt.legend()
plt.grid(True)
plt.show()
正态分布残差的问题
线性回归的另一个局限性是其假设残差(观测值与预测值之间的差异)呈正态分布。这个假设在计数数据上往往不成立,尤其是当平均计数较低时,会导致分布偏斜。计数数据的分布通常是偏斜的,不像正态分布那样对称。
让我们在Python中演示这一点。
# Calculating residuals
y_pred_actual = model.predict(x.reshape(-1, 1))
residuals = y - y_pred_actual
# Plotting residuals
plt.hist(residuals, bins=20, color='grey', edgecolor='black')
plt.axvline(0, color='red', linestyle='--')
plt.xlabel('Residuals')
plt.ylabel('Frequency')
plt.title('Distribution of Residuals in Linear Regression')
plt.grid(True)
plt.show()
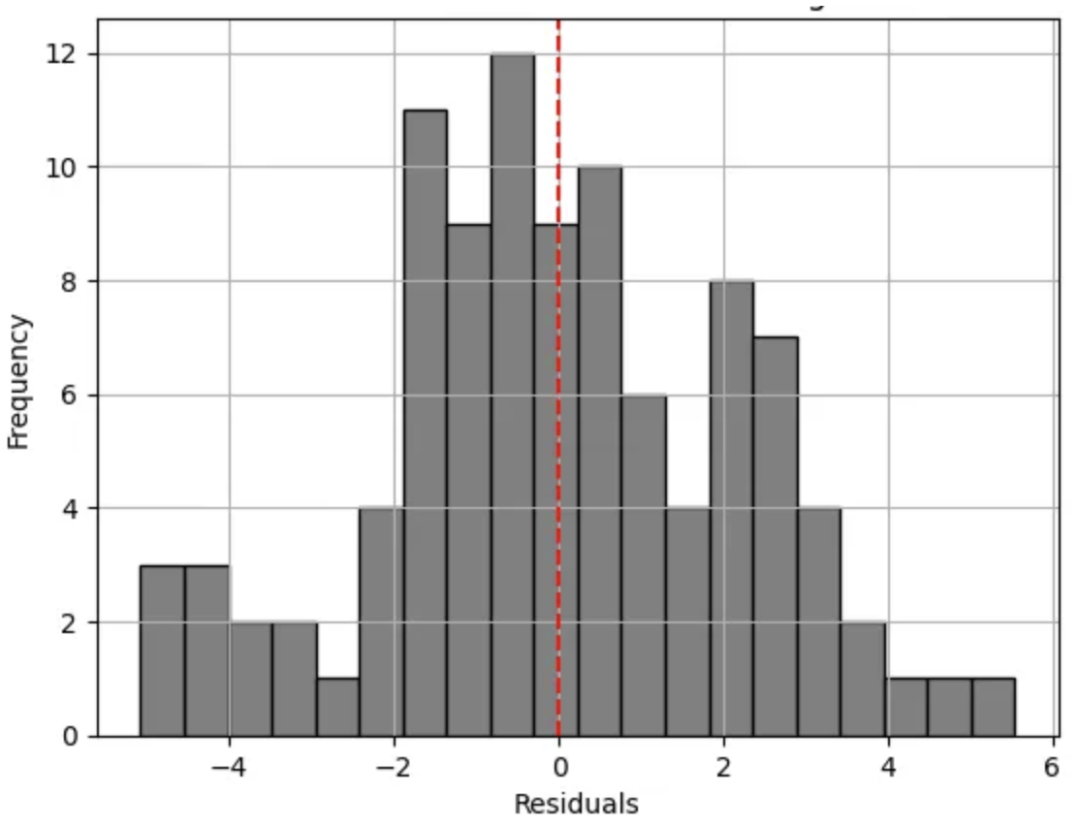
观察上述直方图,我们可以立即观察到它的多峰(即存在多个峰值)特征。因此,这一特征使我们偏离了预期的钟形分布(对于正态分布的残差)。由此,我们可以清楚地看到这已经违反了线性回归的假设。
另一个需要注意的关键点是残差的扩散。观察直方图时,我们可以看到它相当宽——表明方差变化较大。对于一个拟合良好的模型,残差的扩散应该尽可能窄(即预测值接近实际值)。
以上几点表明,简单线性模型并未充分捕捉到关系。此外,轻微的偏斜和潜在的异常值指出了模型在为所有观测值做出准确预测方面的局限性。
深入探讨泊松回归
当我们处理计数数据时,泊松回归确实能提供很大帮助。计数数据本质上包含非负整数,而在对此类数据进行建模时,与线性回归相比,泊松回归提供了一个更合适的框架。
理解泊松回归
泊松分布是一种离散概率分布,它表达了在已知的恒定平均率下,固定时间或空间间隔内发生特定数量事件的概率,并且这些事件的发生是相互独立的,不受上一次事件发生以来时间的影响。
泊松分布的关键特性:
均值和方差相等——随着平均发生次数的增加,计数的变异性也随之增加。
它为固定时间或空间间隔内事件发生的次数分配概率,但前提是这些事件发生在恒定速率下且彼此独立。
**泊松回归应用场景
在泊松回归中,我们将预期计数的对数作为自变量的线性函数来建模。
我们可以表示如下:
log(λ) = β0 + β1x1 + β2 * x2 + ... + βnxn
其中 λ 代表预期计数或发生率。
泊松回归模型的解释
泊松回归模型中的系数解释了在保持所有其他预测变量不变的情况下,预测变量每单位变化所导致的预期计数的对数变化。
泊松回归与线性回归之间的主要差异
残差的分布:泊松回归不假设残差呈正态分布;相反,它假设数据遵循泊松分布,这对于计数数据通常更为合适。
处理非负计数:泊松回归固有地处理非负整数计数,确保模型不会预测负数。
让我们用Python来演示如何应用泊松回归。
import numpy as np
import matplotlib.pyplot as plt
import statsmodels.api as sm
# Simulating count data
np.random.seed(0)
x = np.random.normal(5, 2, 100) # Independent variable data
y = np.random.poisson(np.exp(x * 0.1)) # Simulated count data
# Poisson Regression Model
exog, endog = sm.add_constant(x), y
poisson_model = sm.GLM(endog, exog, family=sm.families.Poisson()).fit()
# Predictions and plot
x_test = np.linspace(min(x), max(x), 100)
y_pred = poisson_model.predict(sm.add_constant(x_test))
plt.scatter(x, y, color='blue', label='Actual Count Data')
plt.plot(x_test, y_pred, color='red', label='Poisson Regression Predictions')
plt.xlabel('Independent Variable (x)')
plt.ylabel('Expected Count (y)')
plt.title('Poisson Regression on Count Data')
plt.legend()
plt.grid(True)
plt.show()
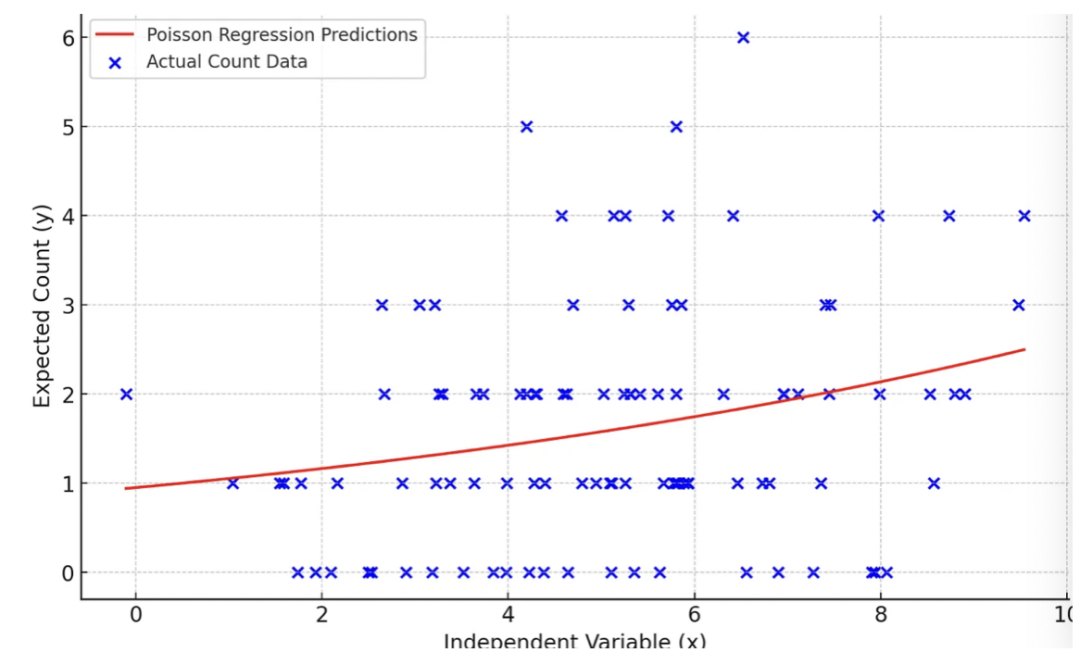
一些关键观察结果:
预测线(红色)不是直线。这表明了自变量和预期计数之间的对数关系,这是泊松回归的一个关键特征。
该模型预测,随着 x 的增加,预期计数(y)也增加,但不是以恒定速率增加(由于对数链接函数)。
与线性回归不同,泊松回归模型不预测负数计数。所有预测值都是非负的,这对于计数数据是合适的。
预测线似乎捕捉到了实际数据的一般趋势,表明这个模拟数据集有一个合理的拟合。这清楚地展示了泊松回归在建模计数数据时的适用性。
这清楚地展示了泊松回归在建模计数数据时的适用性。
该模型考虑了计数的非负性和它们的分布性质。
与线性回归不同,泊松回归可以处理计数数据的方差结构,其中方差与均值成正比,使其成为计数数据分析的有力工具。
结论
关键点回顾
在本文中,我们探讨了线性回归的基本方面以及其在应用于计数数据时的局限性。
我们发现线性回归可能预测出负值,并对残差的分布做出假设,这些假设对于本质上是非负的且通常是偏斜的计数数据并不成立。然后,我们引入了泊松回归作为计数数据的健壮替代方案。泊松回归旨在处理非负整数,并适应数据中特有的计数方差。
模型选择的重要性
统计模型的选择至关重要,可以显著影响从数据中得到的洞察。
理解数据的本质和不同模型背后的假设至关重要。
通过选择最适合数据特征的模型,我们确保更准确、可靠和有意义的预测。
审核编辑:刘清
全部0条评论

快来发表一下你的评论吧 !
