

嵌入式设计应用
单精度数是指计算机表达实数近似值的一种方式。VB中Single(单精度浮点型)变量存储为 IEEE 32 位(4 个字节)浮点数值的形式,它的范围在负数的时候是从 -3.402823E38 到 -1.401298E-45,而在正数的时候是从 1.401298E-45 到 3.402823E38 。
在计算机里实数中的浮点数是以科学计数法存储,所以在存储和读取的时候需要考虑精度的问题,但是,由于数据的使用需要,也会有不同精度的需要,例如存储身高信息和存储卫星的飞行信息要求的精度必要是不一样的,再者,考虑存储信息的效率问题,同样大小的存储介质存储高精度的信息必然比低精度的信息要多,为了平衡,所有就有单精度float和双精度double,同样是61.1126537这个数,经过计算机处理后用float存储和赌博了存储是不一样的。
如果a》0,那么1+a一定大于1吗?在数学上,答案是肯定的。但在计算机上,答案就与a的大小和浮点数的精度有关了。在matalb上,可以作以下计算:
》》 a=1/2^52
a =
2.220446049250313e-016
》》 1+a》1
ans =
1
》》 a=1/2^53
a =
1.110223024625157e-016
》》 1+a》1
ans =
0
可见,当a等于1/2^53时,1+a》1是不成立的。
IEEE754定义了单精度浮点数和双精度数浮点数,即float和double。float有32bit,double有64bit。它们都包括符号位、指数和尾数。
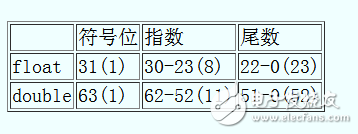
符号位有1bit,0表示正、1表示负。设一个数的指数是e,指数部分的值是bias+e。加上一个bias是为了表示负数。 float的bias是127,double的bias是1023。指数全0或全1有特殊含义,不算正常指数。
float的指数部分有8bit,可以取值1~254,减掉127,得到对应的指数范围-126~127。
double的指数部分有11位,可以取值1~2046,减掉1023,得到对应的指数范围-1022~1023。
这里的指数是以2为底的,同样尾数也是二进制的。IEEE754要求浮点数以规范形式存储,即小数点前有1位非零数字。 对于二进制数,非零数字只有1。所以IEEE754在存储时省略了这个小数点前面的1,只存储小数点后面的位。
看个例子,设:
double a=0.2;
在PC上,我们可以看到a对应的存储区数据是:
9A 99 99 99 99 99 C9 3F
PC的数据是小尾的,即低位字节在后,将其写成高位字节在前,得到:
3F C9 99 99 99 99 99 9A
可见符号位为0。指数位是0x3FC,即1020,减掉1023,得到指数-3。尾数是999999999999A。所以完整的数字就是16进制的1.999999999999A乘上2^-3。即:
a=(1+9*(1/16+1/16^2+.。.+1/16^12)+10/16^13)*2^-3
(1/16+.。.+1/16^12)可以用等比级数求和公式a1*(1-q^n)/(1-q)计算,其中a1=1/16,q=1/16,n=12,因此:
a=(1+9*(1-1/16^12)/15+10/16^13)*2^-3
用windows的计算器计算上式,得到
a=0.2000 0000 0000 0000 1110 2230 2462 5157
这也不是精确解,但已经可以看到用double表示0.2时存在的误差。这个例子说明在用有限字长的二进制浮点数表示任意实数a可能引入误差。 设实数a的指数为e,尾数位数为n,显然:
误差《(1/2^n)*2^e
可以把机器精度定义为满足条件
fl(1+ε)》1
的最小浮点数ε。其中fl(1+ε)是1+ε的浮点表示。显然double的机器精度是1/2^52。float的机器精度是1/2^23。 matlab内部采用double,1+1/2^53对double来说就是1,所以1+1/2^53不会大于1。
对于规范数来说,因为小数点前默认有个1,所以float的有效数字是24bit,对应8位十进制有效数字; double的有效数字是53bit,对应16位十进制有效数字。
前面提到浮点数的指数全0或全1有特殊含义,让我们来看看这些特殊的浮点数:
指数和尾数都是全0表示0。根据符号位不同可以分为+0和-0。
指数全0,尾数不为全0,这些数是非规范数,即尾数部分不假设前面存在小数点前的1。 或者说这些数太接近0了,因为指数已经不能再小,所以这些数不能写成规范形式。 例如:double数0000 0000 0000 0001的尾数是0 0000 0000 0001,即1/2^52,对应的数是1/(2^52)*2^-1022,即4.9406564584124654e-324。
指数全1,尾数全0表示无穷大,即inf。根据符号位不同可以分为+inf和-inf。
指数全1,尾数不为全0表示NaN,即Not a Number,不是数。尾数最高位为1的NaN被称作QNaN(Quiet NaN)。 尾数最高位为0的NaN被称作SNaN(Signalling NaN)。通常用QNaN表示不确定的操作,用SNaN表示无效的操作。
在计算机内部,double就是一个64位数。从0x0000 0000 0000 0000~0xFFFF FFFF FFFF FFFF,每个64位数都对应一个浮点数或NaN。 我写了一个小程序,按照64位无符号整数的顺序打印出典型的浮点数。 表格的第一列是浮点数的内部表示。为了便于阅读,按大尾顺序输出。第二列是对应的浮点数。 第三列是注释,对于非规范数和规范数给出了由内部表示计算数值的matlab算式。 注意在C/C++中,2^52要写成pow(2.0,52.0)。

从表中可以看到,double内部表示的设计是很有规律的,按照对应64位数的顺序依次为 +0、正非规范数、正规范数、正无穷大、符号位为正的NaN、-0、负非规范数、负规范数、负无穷大、符号位为负的NaN。
double内部表示的设计保持了浮点数的有序性。即:如果正double数a《正double数b,则a对应的64位无符号整数《b对应的64位无符号整数。 负数因为差了个符号,所以浮点数与对应整数的顺序相反。 float也有类似的规律。
float和int都是32bit,但float的尾数只用了23bit。int的精度高于float,float的表示范围大于int。float牺牲精度换取了更大的表示范围。 double的尾数是52bit,高于32bit的int,所以用dobule表示int不会有精度损失。 double是科学计算的常用类型,了解double的内在和限制,有助于我们更好地使用它。
全部0条评论

快来发表一下你的评论吧 !
