

模拟技术
ADI专利的容性可编程增益放大器(PGA)相比传统的阻性PGA具有更佳的性能,包括针对模拟输入信号的更高共模电压抑制能力。
本文描述了斩波容性放大器的工作原理,强调了需要放大传感器小信号至接近供电轨——比如温度测量(RTD或热电偶)和惠斯登电桥——时,此架构的优势。
Σ-Δ型模数转换器(ADC)广泛用于传感器具有较小输出电压范围和带宽的应用中(比如应变计或热敏电阻),因为这种架构提供高动态范围。具有高动态范围是因为,相比其它ADC架构,它具有低噪声性能。
Σ-Δ型转换器基于两条原理工作:过采样和噪声整形。当ADC对输入信号进行采样时,独立于采样频率的量化噪声会在直到采样频率一半的整个频谱内扩散。因此,如果输入信号以比奈奎斯特理论所推导出的最小值高很多的频率采样,则目标频段内的量化噪声下降。
图1显示了不同采样频率下的量化噪声密度示例。
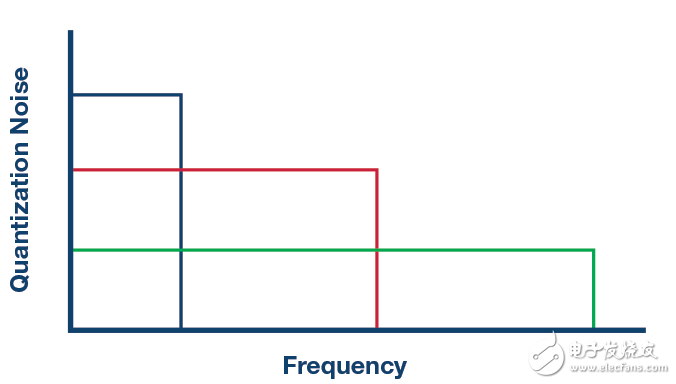
图1.不同采样频率下,频率范围内的量化噪声密度。
一般而言,对于特定的目标频段,每2个过采样系数就会使动态范围改善3dB(假定为白噪声频谱)。Σ-Δ型转换器的第二个优势是噪声传递函数。它将噪声整形至更高频率(如图2所示),进一步降低了目标频段内的量化噪声。
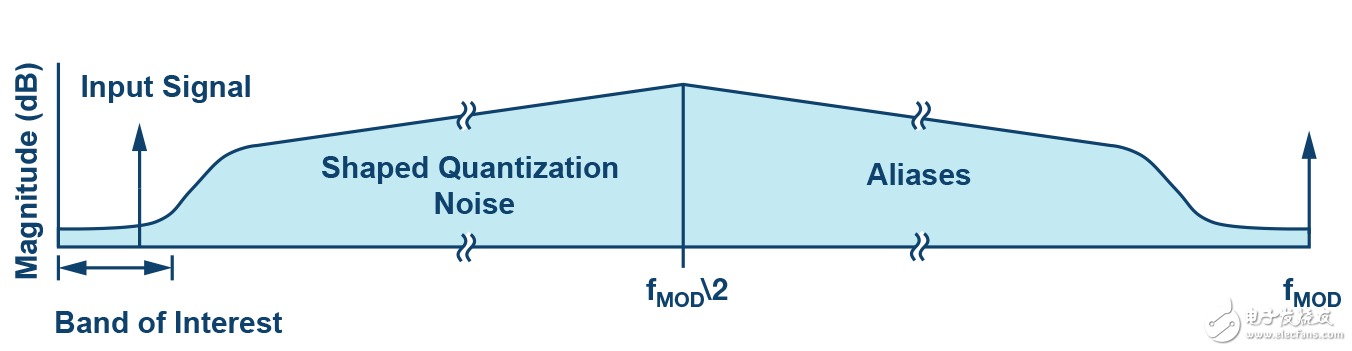
图2.Σ-Δ噪声整形
此外,Σ-Δ架构可能集成数字滤波器,用来移除目标频段外的量化噪声,实现出色的动态范围性能,如图3所示。

图3.LPF之后的量化噪声。
过采样架构的缺点之一是,相比其它采样频率较低的架构,驱动Σ-Δ型调制器的输入缓冲器要求可能会更严格。采集时间变得更短,因此缓冲器需要更高带宽。现代Σ-Δ型转换器片上集成输入缓冲器,最大程度简化使用
此外,在检测系统中,为检测元件提供具有高精度的极高输入阻抗对于测量精度而言极为关键。这使得输入缓冲器的要求更为严格了。
集成输入缓冲器还有其它挑战。Σ-Δ型调制器可在低频率时提供极低噪声,但所有其它元件(比如输入缓冲器)都会使热噪声增加,而更严重的则是低频闪烁噪声,如图4所示。
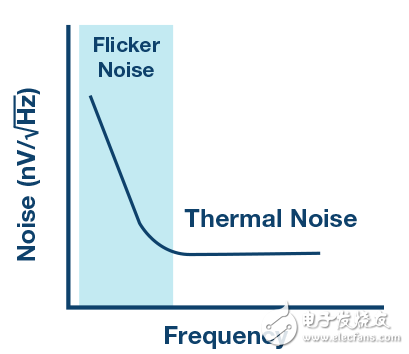
图4.闪烁噪声。
此外,缓冲器失调也可能增加总系统误差。通过系统校准可以补偿失调,但如果失调漂移相对较高,那么这种方式就无法实现,因为每次工作温度发生改变都会要求系统重新校准,以补偿缓冲器失调。
例如,当失调漂移为500 nV/°C时,10°C温度递增将等于5 μV失调范围,在±2.5 VREF 24位ADC中这相当于16.8 LSB,即约为4位。
解决这两个问题的典型途径是对缓冲器的输入和输出进行斩波,如图5所示。
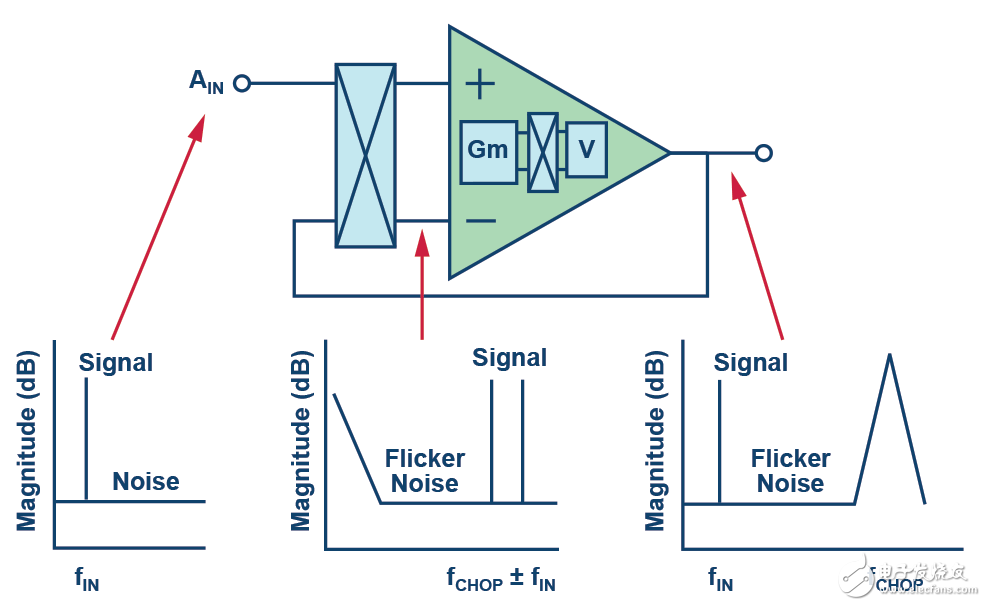
图5.斩波放大器。
对输入进行斩波之后,输入频率便调制到较高频率。缓冲器失调和闪烁噪声依然保持其最初的低频率,因为它们不受输入斩波的影响。
输出去斩波机制将输入频率解调回基带,同时向上调制缓冲器产生的失调和闪烁噪声至较高频率,随后由ADC低通滤波器加以消除。
某些情况下,输入缓冲器可以采用基于电阻的仪表放大器(阻性PGA)来代替,以使小传感器信号满足全调制器输入范围,最大程度提升动态范围。需注意,基于电阻的仪表放大器相比差分阻性放大器是更好的选择,因为分立式传感器需要更高的输入阻抗。阻性PGA可实现类似的斩波方案,如图6所示。
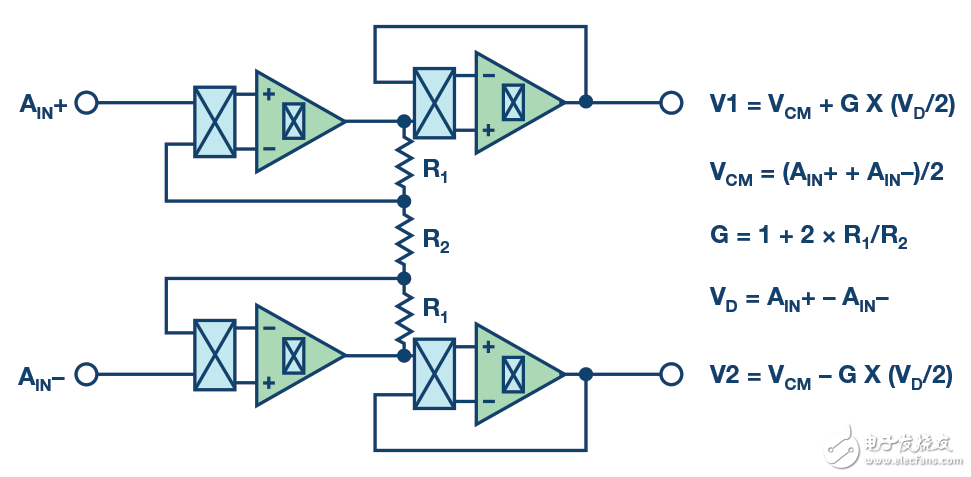
图6.阻性PGA。
阻性PGA可能需要级联第二组缓冲器,因为放大器可能无法提供直接驱动调制器所需要的足够带宽。同时,必须保持低功耗,这就确定了电阻值,进而确定了放大器带宽。
使用这种放大器拓扑的主要问题是,它限制了共模电压——尤其是在增益大于1的时候,因为阻性PGA具有取决于输入信号的浮动共模值,如图6所示。
此外,阻性网络失配及其漂移也是影响总误差预算的因素之一,因为它可能会影响大多数的精度规格。
为避免这些限制,最新的Σ-Δ型转换器采用了容性PGA。
容性PGA放大原理与阻性PGA相似:增益取决于电容比,如图7所示。
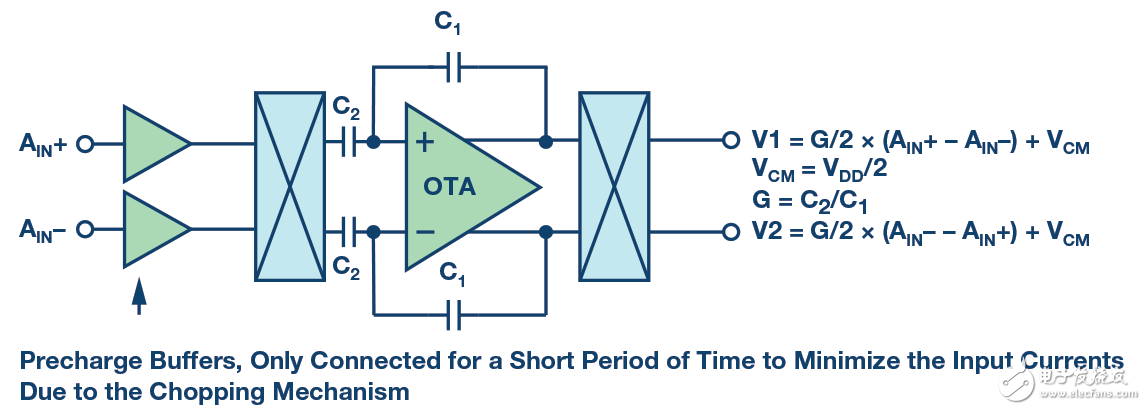
图7.容性PGA(为简便起见,移除了部分模块)。
为了放大直流信号,容性PGA在PGA输入端引入了斩波机制直流输入信号调制到斩波频率,然后由容性放大器进行放大。最后,信号通过输出去斩波解调回直流。此外,放大器失调和闪烁噪声调制到斩波频率,并在之后的级中进行低通滤波。
相比阻性架构,这种容性架构有一些优势:
它能更好地权衡噪声与功率,因为噪声源较少。需要较少的放大器,而且相比电阻,电容不会产生噪声。
电容比电阻有非常多的优势。除了无噪声外,电容不会受到自发热影响,且通常具有更好的匹配和温度漂移。这对失调、增益误差和漂移规格有正面影响。
电容可将输入共模从信号链共模的其余部分去耦。这样可以提供CMRR、PSRR和THD等优势。
容性PGA的最大优势之一,是它的输入共模范围可以是轨到轨或更高。这样便有可能从正供电轨下至负供电轨的几乎任何地方对传感器共模电压进行偏置。
这种容性架构结合了仪表放大器的优势,具有极高的输入阻抗(因为输入阻抗是一个电容),其优势是电容(而不是电阻)作为增益元件,增加了放大器的动态范围——这不仅是因为它的信号摆幅,还因为其噪声效率的缘故。
克服阻性PGA共模限制的常见解决方案是增加或偏移供电轨,或者重新对中传感器信号共模。这样做的代价是功耗更高、电源设计更复杂、使用更多外部元件,以及更高的成本。
在惠斯登电桥中,共模电压由连接两个桥臂的阻抗决定,且与施加的电源成正比。电子秤应用即采用这种检测拓扑,因为它具有针对应变计的线性检测优势;图8显示了一个半桥式II类电路。
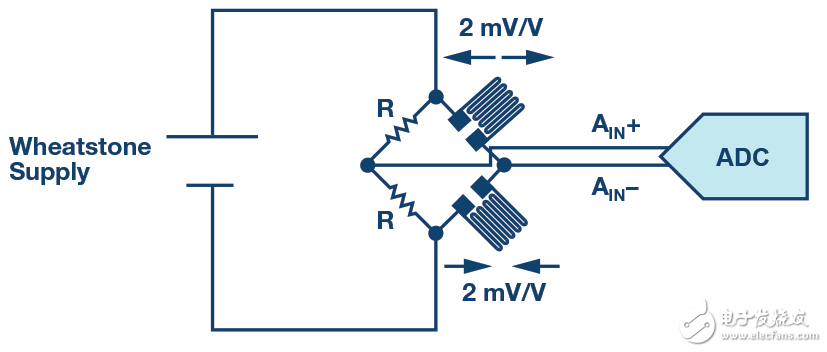
图8.采用惠斯登拓扑并包含应变计的电子秤。
应变计的灵敏度通常为2mV/V。惠斯登电源越高,灵敏度也就越高。为了增加应变计的动态范围并最大化SNR,电桥可能采用比ADC更高的电源供电。
由于阻性PGA的共模限制,电桥应当采用与ADC相同的电源供电,以便最大程度提升动态范围;而在容性PGA中,电桥可以采用几乎为ADC两倍的电源供电,因为不存在输入共模的限制。
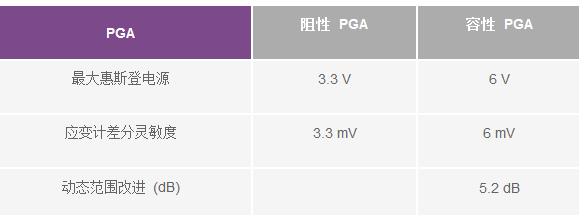
例如,假设标准电源为ADC提供3.3V电平,则对于相同的增益,容性PGA相比阻性PGA的改进总结见表1。
表1. 惠斯登电桥中的阻性PGA和容性PGA对比(假设使用标准电源和增益)
可能存在的另一个问题,是当电桥的连接位置离ADC较远时,接地之间可能有所不同。这也许会使共模电压偏移,从而导致ADC输入共模相对于电桥不平衡,并降低阻性PGA中的最大允许增益。
使容性PGA性能与阻性PGA相当的可行办法是以更高的电源电压对电桥供电。比如,以±3.3 V双极性电源对电桥供电,从而增加应变计的灵敏度,但代价是更高的系统复杂性和功耗。
可能会得益于容性PGA的另一个例子是采用电阻式温度检测器(RTD)或热电偶的温度测量应用。
常用RTD电阻(比如PT100)可以用来直接检测温度,或间接检测热电偶的冷结,如图9所示。
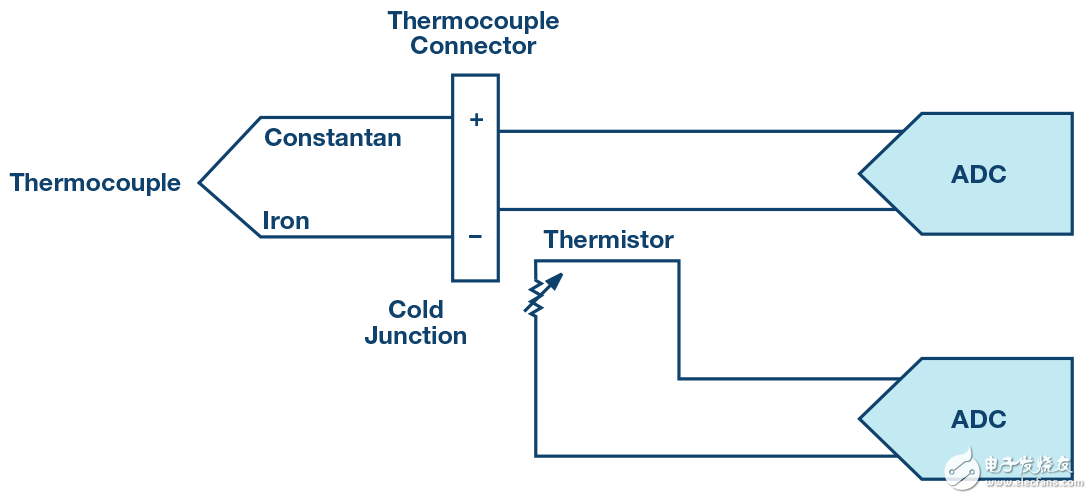
图9.典型热电偶设置。
每一个PT100器件都提供不同的导线,采用最受欢迎的高性价比三线式配置。
测量温度并消除引线误差的传统方法如图10所示。本例中,集成PGA的Σ-Δ型ADCAD7124-8的内部电流源以相同电流驱动双线式RTD,在两个引线上产生相同的失调误差,其值与引线电阻成正比。
由于 AD7174-8 具有较小的引线电阻和电流(为了最大程度减少自发热效应),RL3产生的失调电压靠近负供电轨,极大地降低了阻性PGA中允许的最大增益,因为其输入共模相比容性PGA同样将会非常接近供电轨,在内部将共模电压设为电源供电轨的一半,允许更高的增益配置,从而提高总动态范围。
建议的解决方案极大降低了系统和硬件连接的复杂性,因为第三条线缆不应返回至ADC PCB,并可连接RTD位置附近的地。
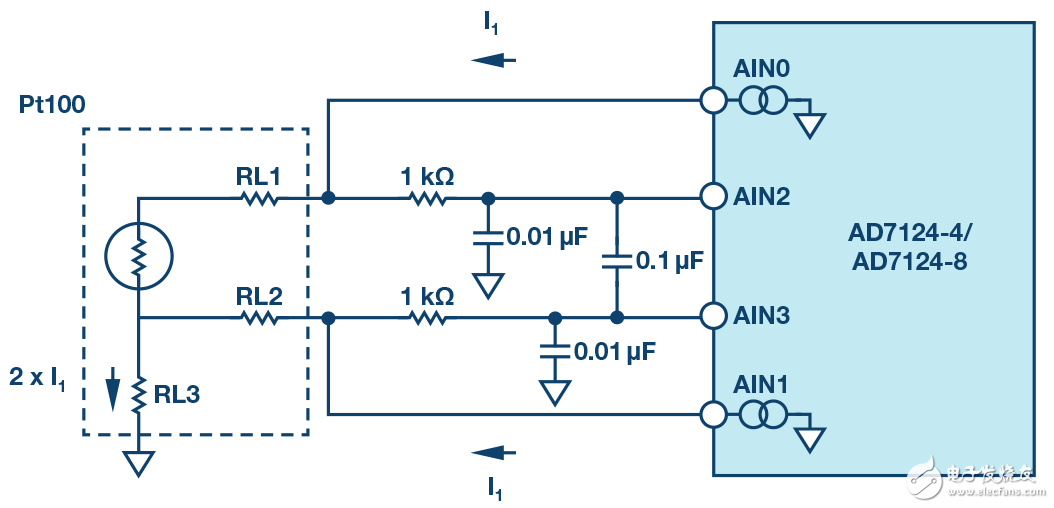
图10.三线式RTD测量。
为了增加温度测量的精度,建议采用四线式测量。本例中,只使用了一个电流基准。为了避免电流源的不精确性,可以将精密电阻用作ADC基准电压发生器来进行比例测量,如图11所示。
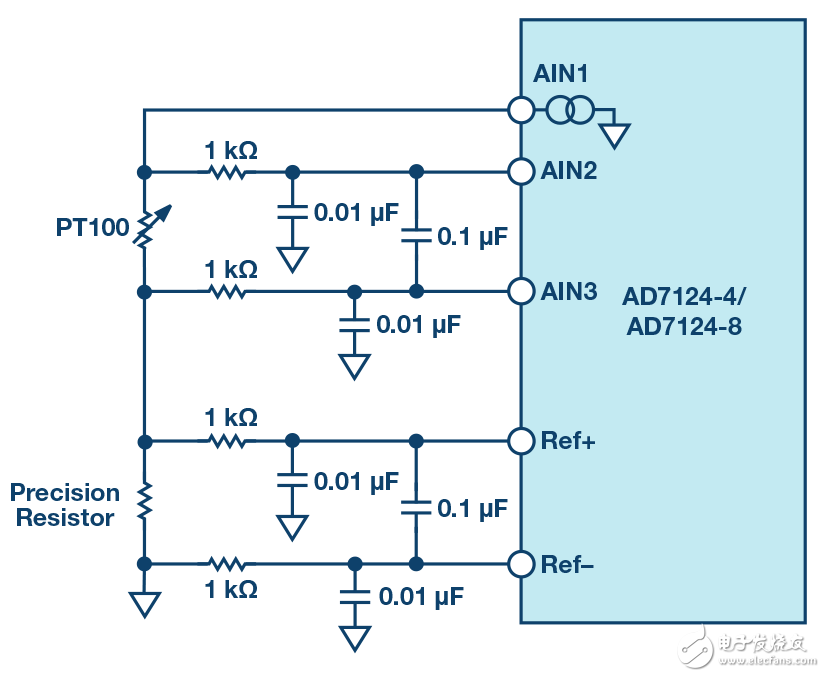
图11 。比例四线式RTD测量。
选择适当的外部精密电阻值,使RTD上产生的最大电压等于基准电压除以PGA增益。
对于3.3 V电源而言,在阻性PGA中,精密电阻上产生的电压应为1.65 V左右,否则PGA共模电压将限制最大增益。其结果是,最大增益信号应等于1.65V。在容性PGA中,不存在输入共模的限制,因此RTD共模信号可以靠近顶部供电轨放置,最大程度提升了精密电阻生成的ADC基准电压,并因此实现最高的可选增益和动态范围。
表2总结了阻性PGA相对于容性PGA的最大增益,最大电流源为500μA,限制了Pt100的自发热(假定B类RTD,此时最高温度为600°C,最大VREF为2.5 V)。
表2. 四线式RTD比例测量中的阻性和容性PGA对比
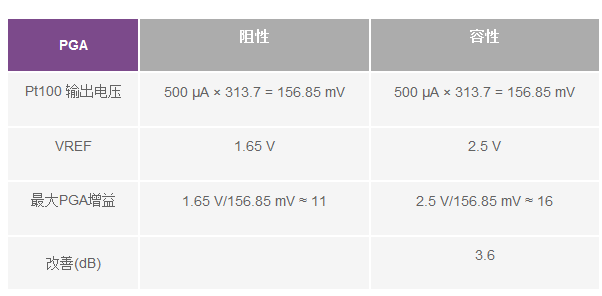
相比阻性PGA,容性PGA具有多项重要优势。诸如噪声、共模抑制、失调、增益误差以及温度漂移等关键规格都由于电容作为增益元件的固有温度稳定性以及匹配属性而得到了改善。
另一项重要特性是内部共模电压从放大器内部共模电压中去耦。当待放大的输入信号为靠近供电轨的共模电压时,这点尤为重要。阻性PGA的增益选择严重受限于其共模限制,或者要求更高的供电轨或外部元件将输入信号重新偏置到供电轨的一半。而容性PGA却可以轻松处理这种检测场景。
某些最新的Σ-Δ型ADC产品集成了容性PGA,比 如 AD7190, AD7124-4, AD7124-8, and AD7779.
全部0条评论

快来发表一下你的评论吧 !
