

节点电压分析发现不同节点之间的电路周围未知电压降,为两个或多个电路元件提供公共连接
节点电压分析补充了以前的网格分析,它同样强大,并基于相同的矩阵分析概念。顾名思义,节点电压分析使用Kirchhoff第一定律的“Nodal”方程来找出电路周围的电压电位。
所以通过将所有这些节点电压加在一起净结果将等于零。然后,如果电路中有“n”个节点,则会有“n-1”个独立的节点方程,仅这些就足以描述并因此解决电路。
在每个节点处写下Kirchhoff的第一定律方程,即:“进入节点的电流与离开节点的电流的值完全相等”然后根据分支上的电压表示每个电流。对于“n”个节点,一个节点将用作参考节点,所有其他电压将相对于该公共节点进行参考或测量。
例如,考虑上一节中的电路。
节点电压分析电路
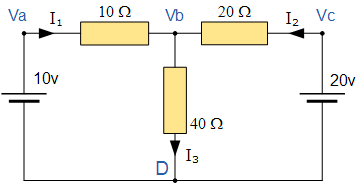
在上面的电路中,节点 D选择作为参考节点,假设其他三个节点相对于节点 D具有 Va,Vb 和 Vc 的电压。例如;
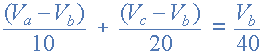
当 Va = 10v 且 Vc = 20v , Vb 可以通过以下方式轻松找到:
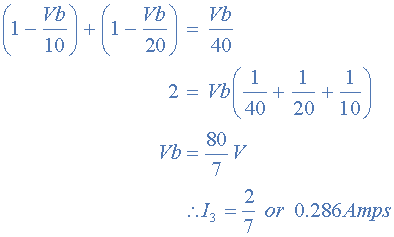
相同的 0.286amps 值,我们在前一个教程中使用了Kirchhoff的Circuit Law。
从我们到目前为止看到的网格和节点分析方法来看,这是最简单的解决这个特定电路的方法。通常,当周围存在大量电流源时,节点电压分析更合适。然后将网络定义为:[ I ] = [ Y ] [ V ]其中[ I ]为驱动电流源[ V ]是要找到的节点电压,[ Y ]是在[ V 上运行的网络的导纳矩阵]给[ I ]。
节点电压分析摘要
求解Nodal分析方程的基本步骤如下:
1。记下当前向量,假设流入节点的电流为正。即,“N”个独立节点的( N x 1 )个矩阵。
2.写入导纳矩阵[网络的Y ]:
Y 11 =第一个节点的总导纳。
Y 22 =第二个节点的总导纳。
R JK =总数准入加入节点 J 到节点 K 。
3。对于网络“N”个独立节点,[ Y ]将是( N x N )矩阵, Ynn 将为正且 Yjk 将为负值或零值。
4。电压矢量将为( N x L )并列出要找到的“N”电压。
我们现在已经看到了许多简化线性电路分析的定理。在下一个教程中,我们将看看Thevenins定理,该定理允许由线性电阻和源组成的网络由具有单个电压源和串联电阻的等效电路表示。
全部0条评论

快来发表一下你的评论吧 !
