概要:本文以一简单的单孔销浮动案例用理论计算结果与模拟
仿真计算结果做对比,验证了仿真计算的精度,同时为我们公差仿真计算提供一个理论校核的可借鉴步骤。我们不仅关注公差仿真建模,并且还探讨深挖其背后的理论知识。
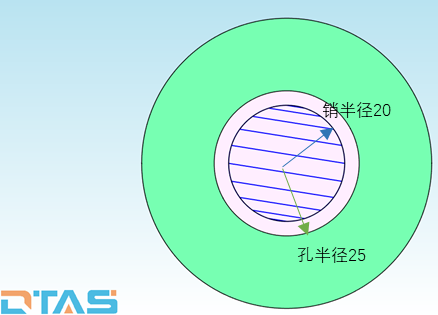
上节中我们回答了如下问题:
问题: 假设孔销直径公差不考虑,孔销相切浮动时,销在竖直方向的波动量为多少?
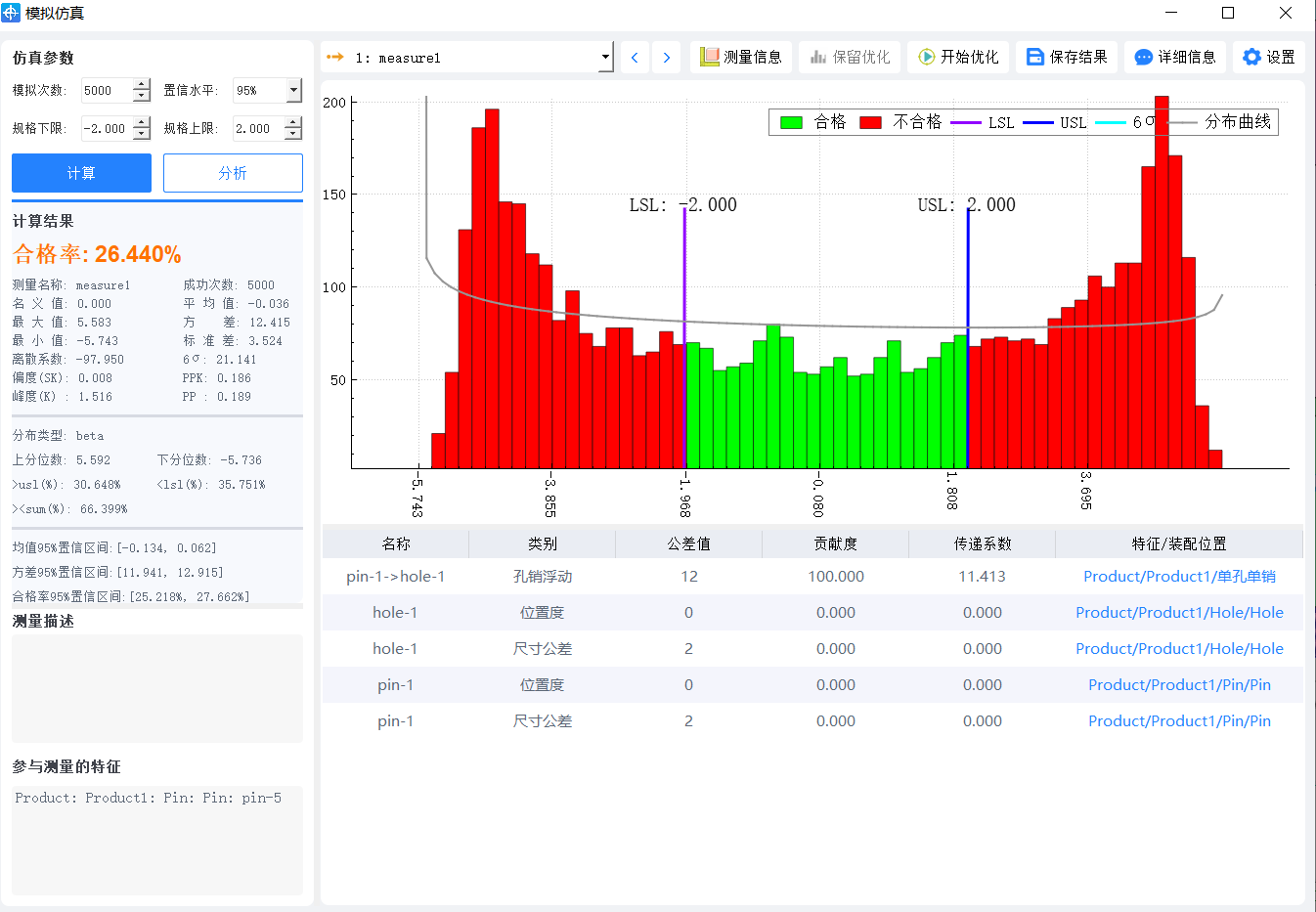
我 们用DTAS 3D 建立孔销虚拟装配和沿着竖直方向的虚拟测量 ,我们用蒙特卡洛方法模拟5000次,动画模拟如上图所示,各种统计参数结果如下图所示,最大值最小值为±5,均值接近0,方差为12.517,柱状图拟合分布曲线形状奇特,不是正态分布。(仿真结果会随着初始随机种子的不同略有不同)。
仿真动画
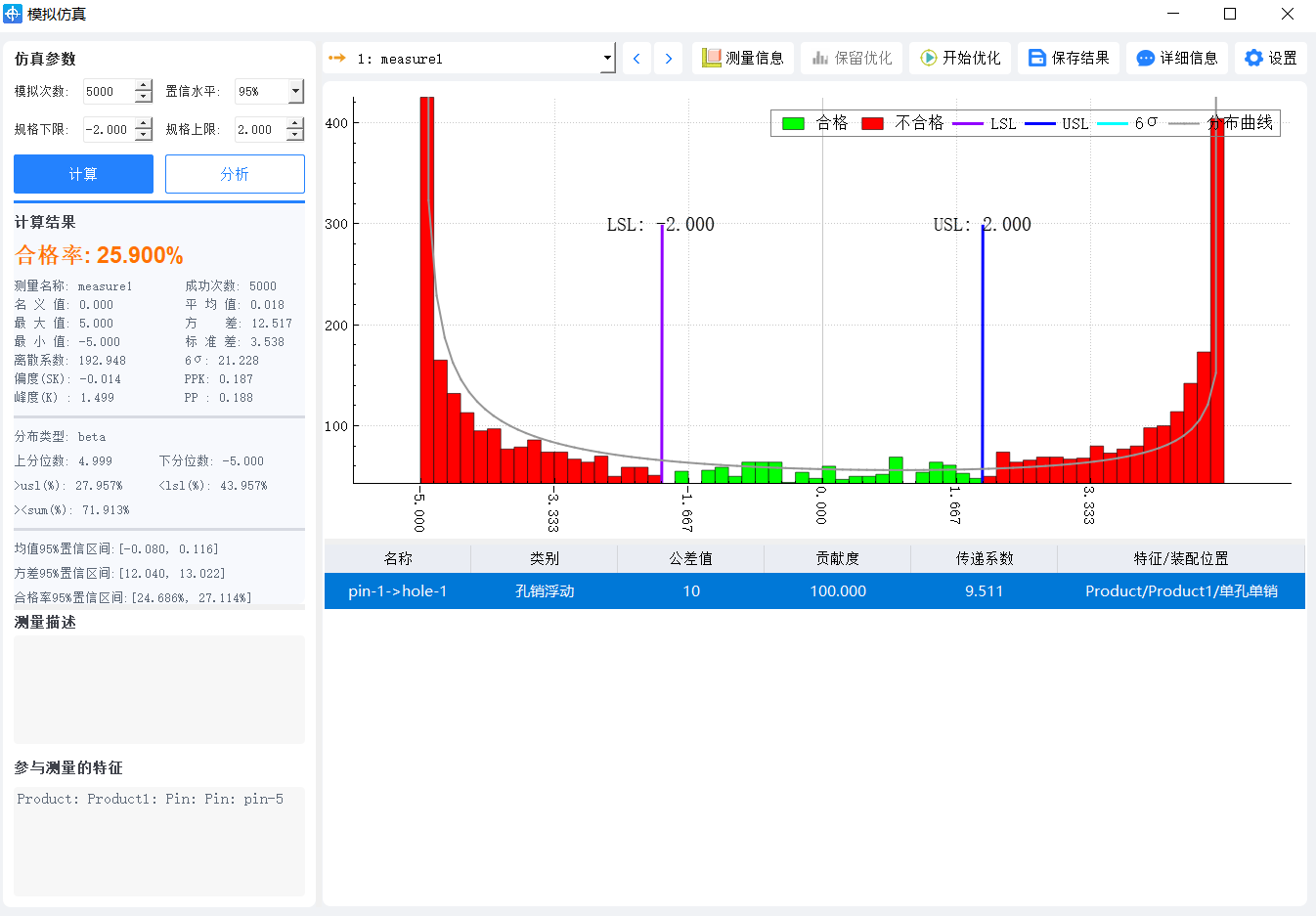
仿真结果
这节中我们孔销直径公差不考虑,孔销改为均匀浮动,继续探讨销在竖直方向的波动。
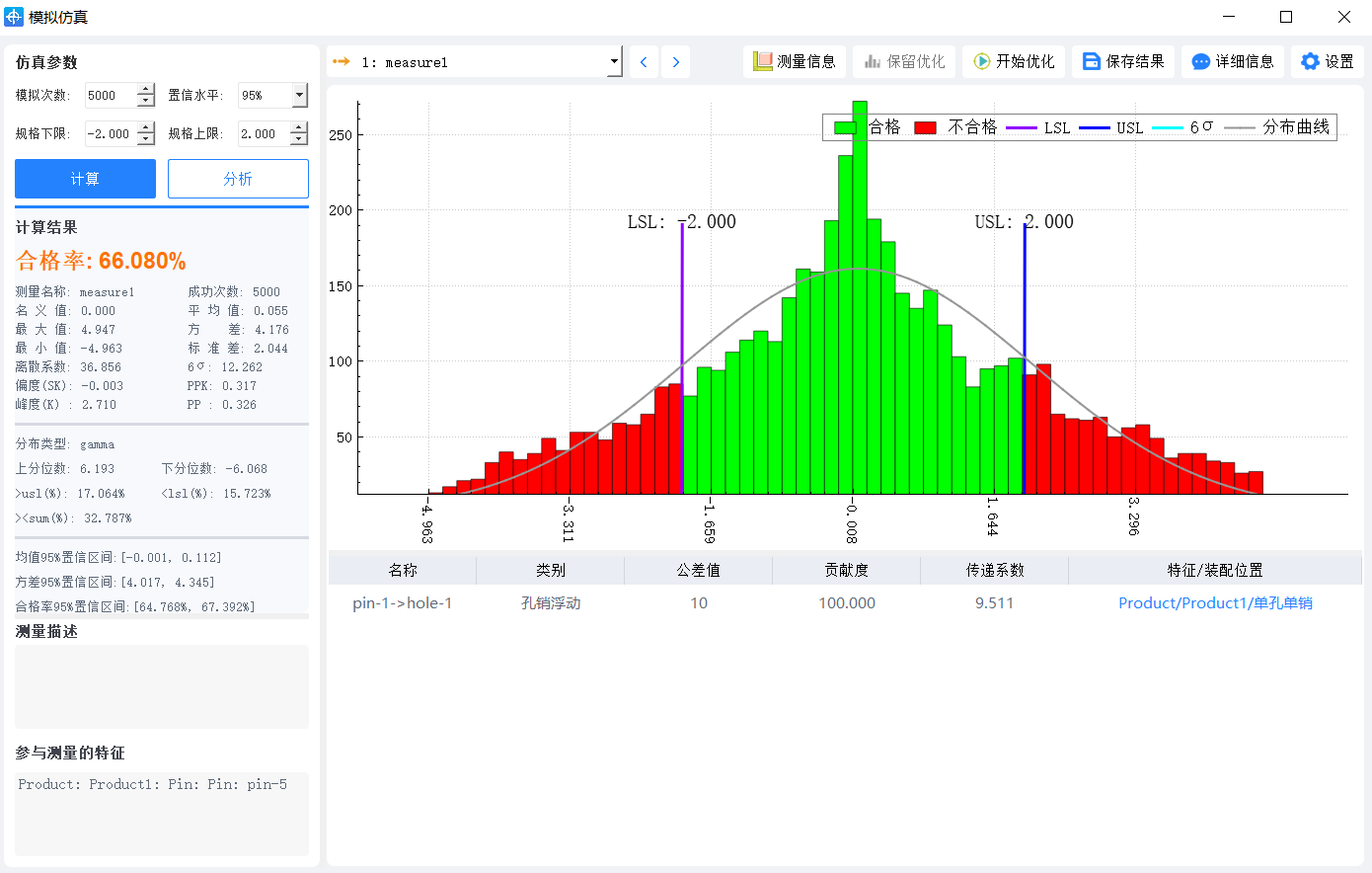
改为均匀浮动后,平均值基本接近为0 方差为4.176,数据分散变好。接下来我们理论推导4.176如何得来的。
一、数学模型
本案的实际问题转化为如下数学模型:
已知随机变量的概率密度函数(pdf)为:
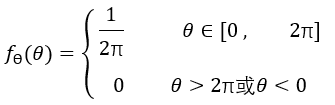
随机变量R为均匀分布,其概率密度函数(pdf)为:
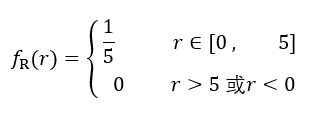
那么随机变量Y=R*sinθ的分布统计参数分别是多少呢?
二、均值、方差及标准差的理论计算
数学上本质是两个随机变量的积的分布,是一个二维联合概率分布。
从上一节我们得知R的期望为5/2 ,方差为
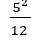
,sinθ的期望为0,方差为1/2。
由于“R”和“θ” 相互独立,
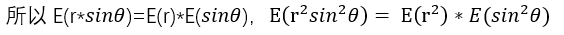
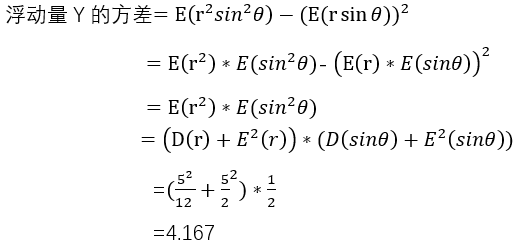
因此标准差的理论值为
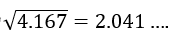
, 模拟仿真计算结果为2.044,仿真精度满足工程需求。
如果问题变为孔销直径各有±1的偏差,且假设直径公差为6σ水平,且为相切浮动。此问题中R就变为一个正态分布,同样的方法我们可推导知标准差的理论值为3.539。
三、工程应用的思考
1. 文中的案例简单 但为我们其它的公差仿真计算提供一个理论校核的借鉴步骤。即建立数学模型,然后运用数学知识求解新的随机变量的累积分布函数、概率密度函数、期望方差等,然后与计算结果作对比。 利用同样的方法我们也可以去推导解释为什么在三维公差仿真分析中当我们用幅度与角度两个随机量做位置度模拟时,幅度通常设置为偏度分布。有兴趣的可以进行尝试推导说明。当然了随着模型的复杂,数学模型的建立很困难,这时候就需要借助专业软件。大多数数值模拟仿真有一定的使用条件或假设,具备一定的理论知识对辨别计算结果的合理与否有很大的帮助。
2. 在本案例中我们为了模拟销在孔当中的浮动,假设了浮动副值在R的范围内均匀分布,以此来模拟销在孔中位置的均匀性,但真实情况如此吗?后续我们将讨论如何真正的模拟销在孔中位置的均匀性,以最大可能的接近实际。



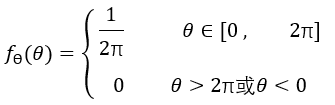
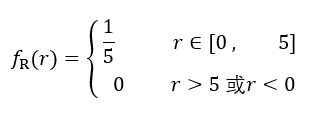
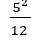 ,sinθ的期望为0,方差为1/2。
,sinθ的期望为0,方差为1/2。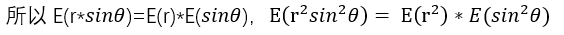
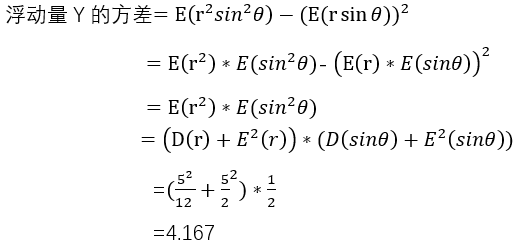
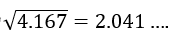 , 模拟仿真计算结果为2.044,仿真精度满足工程需求。
, 模拟仿真计算结果为2.044,仿真精度满足工程需求。

